Exercise 3.4 (Factorisation)

Exercise 3.4

1. Factorise the following by taking out the common factor

(i) 18xy −12 yz

(ii) 9x ⁵ y ³ + 6x ³ y² −18x ² y

(iii) x (b − 2c ) + y(b − 2c)

(iv) (ax + ay) + (bx + by)

(v) 2x ² (4x − 1) − 4x + 1

(vi) 3y (x − 2)² − 2(2 − x)

(vii) 6xy − 4 y ² + 12xy − 2 yzx

(viii) a ³ − 3a² + a − 3

(ix) 3y ³ − 48 y

(x) ab² − bc² − ab + c²

Solution:

(i) 18xy − 12yz = (2 × 3 × 3 × y × x) − (2 × 2 × 3 × y × z)

Taking out the common factors 2, 3, y, we get

= 2 × 3 × y (3x − 2z) = 6y (3x − 2z)

(ii) 9x⁵ y³ + 6x³y² – 18x²y  = (3 × 3 × x² × x³ × y × y²) + (2 × 3 × x² × x × y × y) − (2 × 3 × 3 × x² × y)

Taking out the common factors 3, x², y, we get

= 3 × x² × y (3x³ y² + 2xy − 6)

= 3x²y (3x³ y² + 2xy − 6)

(iii) x(b − 2c) + y (b − 2c)

Taking out the binomial factor (b − 2c) from each term, we have

= (b − 2c) (x + y)

(iv) (ax + ay) + (bx + by)

Taking at ‘a’ from the first term and ‘b’ from the second term we have

(ax + ay) + (bx + by) =  a (x + y) + b (x + y)

Now taking out the binomial factor (x + y) from each term

= (x + y) (a + b)

(v) 2x²(4x − 1) − 4x + 1

Taking out −1 from last two terms

2x²(4x − 1) − 4x + 1  = 2x² (4x − 1) − 1 (4x − 1)

Taking out the binomial factor 4x − 1, we get

= (4x − 1) (2x² − 1)

(vi) 3y (x − 2)² – 2 (2 − x)

3y (x − 2)² – 2 (2 − x) = 3y (x − 2) (x − 2) – 2 (−l) (x − 2)

[∵ Taking out −1 from 2 − x]

= 3y (x − 2) (x − 2) + 2(x − 2)

Taking out the binomial factor x − 2 from each term, we get

= (x − 2) [3y (x − 2) + 2]

(vii) 6xy − 4y² + 12xy − 2yzx

6xy + 12xy − 4y² − 2yzx  [∵  Addition is commutative]

= (6 × x × y) + (2 × 6 × x × y) + ((−1) (2) (2) y + y) + ((−l) (2) (y) (z) (x))

Taking out 6 × x × y from first two terms and (−1) × 2 × y from last two terms we get

= 6 × x × y ( l + 2) + (−l) (2) y [2y + zx]

= 6xy (3) − 2y (2y + zx)

= (2 × 3 × 3 × x × y) − 2xy (2y + zx)

Taking out 2y from two terms

= 2y (9x − (2y + zx)) = 2y (9x −2y − xz)

(viii) a³ − 3a² + a – 3 = a² (a − 3) + 1 (a − 3) [∵ Grouping the terms suitably]

= (a − 3) (a² + 1)

(ix) 3y³ – 48y = 3 × y × y² − 3 × 16 × y

Taking out 3 × y

= 3y (y² − 16) = 3y (y² − 4²)

Comparing y² − 4² with a² − b²

a = y, b = 4

a² − b² = (a + b) (a − b)

y^{2 −} 4² = (y + 4) (y − 4)

∴  3y (y² – 16 ) = 3y (y + 4) (y − 4)

(x) ab² − bc² − ab + c²

Grouping suitably

ab² − bc² − ab + c² = b (ab − c²) − 1 (ab − c²)

Taking out the binomial factor ab − c² = (ab − c²) (b − 1) 

2. Factorise the following expressions

(i) x ² + 14x + 49

(ii) y ² − 10 y + 25

(iii) c ² − 4c −12

(iv) m² + m − 72

(v) 4x ² − 8x + 3

Solution:

(i) x² + 14x + 49 = x² + 14x + 7²

Comparing with a² + 2ab + b²  = (a + b)² we have a = x, b = 7

⇒ x² + 2(x)(7) + 7² = (x + 7)²

∴ x² + 14x + 49 =  (x + 7)²

(ii) y² – 10y + 25 = y²  – 10y + 5²

Comparing with a² − 2ab + b²  = (a − b)² we have a = y, b = 5

⇒ y² + 2(y)(5) + 5² = (y − 5)²

∴ y² – 10y + 25  = (y − 5)²

(iii) c²  − 4c − 12

This is of the form ax² + bx + c

Where a = l, b = −4  c = −12, x = c

Now the product ac = 1 × − 12 = −12 and the sum b = − 4

Product = − 72  :  Sum = 1

1 ×  (−12) = −12  :  1 + (−12) = −11

2 × (−6) = −12    :   2 + (−6) =  −4

∴ The middle term − 4c can be written as 2c − 6c

∴ c² − 4c − 12 = c² + 2c − 6c − 12

= c (c + 2) − 6 (c + 2)

Taking out (c + 2)

=> (c + 2) (c − 6)

∴  c² − 4c − 12 = (c + 2) (c − 6)

(iv) m² + m − 72

This is of the form ax² + bx + c

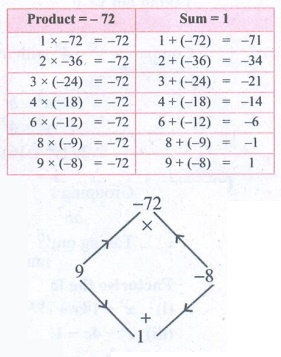
where a = 1, b = l, c = −72

Product a × c = l × −72 = −72

Sum b = 1

The middle term m can be written as 9m − 8m

m² + m – 72 =  m² + 9m – 8m – 72

= m (m + 9) – 8 (m + 9)

Taking out (m + 9)

= (m + 9) (m − 8)

∴ m² + m – 72 = (m + 9) (m − 8)

(v) 4x^{2 −} 8x + 3

This is of the form ax² + bx + c with a =  4 b = − 8  c = 3

Product ac =  4 × 3 = 12

sum b = − 8

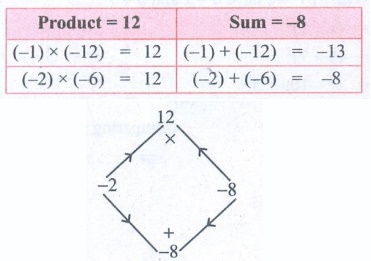
The middle term can be written as − 8x = −2x − 6x

4x² − 8x + 3 = 4x² − 2x − 6x + 3

= 2x (2x − 1) − 3 (2x − 1)

= (2x − l) (2x − 3)

4x² – 8x + 3 = (2x − l) (2x − 3)

3. Factorise the following expressions using (a + b)³ = a ³ + 3a²b + 3ab ² + b³ identity

(i) 64x³+144x² + 108x+27

(ii) 27p³+54p²q+36pq²+8q³

Solution:

(i) 64x³ + 144x² + 108x + 27

= (4x)³ + 3(4x)² (3) + 3(4) (3)² + 3³

= (4x + 3)³

(ii) 27 p³ + 54p²q + 36pq² + 8q³

= (3p)³ + 3(3p)² (2q) + 3(3p) (2q)² + (2q)³

= (3p + 2q)³

4. Factorise the following expressions using (a − b)³ = a ³ − 3a²b + 3ab ² − b³ identity

(i) y³–18y²+108y–216

(ii) 8m³–60m²n+150mn²–125n³

(i) y³ – 18y² + 108y − 216  = y³ – 3y²(6) + 3(6)²y − 6³

= (y − 6)³

(ii) 8m³ – 60 m²n + 150mn² – 125 n³

= (2m)³ − 3(2m)² (5) + 3(2m) (5n)² − (5n)³

= (2m – 5n)³

Objective type Questions

5. Factors of 9x²+6xy are

(A) 3y, (x+2)

(B) 3x, (3x+3y)

(C) 6x, (3x+2y)

(D) 3x, (3x+2y)

[Answer: (D) 3x, (3x + 2y)]

Solution:

9x² + 6xy =  3x (3x + 2y)

6. Factors of 4–m² are

(A) (2+m)(2+m)

(B) (2–m)(2–m)

(C) (2+m)(2–m)

(D) (4+m)(4–m)

[Answer: (C) (2 + m) (2 − m)]

Solution: 4 – m² = 2² − m² 

= (2 + m) (2 − m) 

7. (x+4) and (x–5) are the factors of ___________

(A) x²–x+20

(B) x²–9x–20

(C) x²+x–20

(D) x²–x–20

[Answer: (D) x² – x – 20]

Solution:

(x + 4) (x − 4) = x (x) + 4 (−5) + x (−5) + 4(x)

= x² − 20 − 5x + 4x

= x² − x − 20

8. The factors of x²–5x + 6 are (x–2)(x–p) then the value of p is _________

(A) –3

(B) 3

(C) 2

(D)–2

[Answer: (B) 3]

Solution:

x² − 5x + 6 = x² −3x − 2x + 6

= x (x − 3) – 2 (x − 3)

= (x − 3) (x − 2)

= (x − p) (x − 2)

p = 3

9. The factors of 1–m³

(A) (1+m), (1+m+m²)

(B) (1–m), (1–m–m²)

(C) (1–m), (1+m+m²)

(D) (1+m), (1–m+m²)

[Answer: (C) (1 − m), (1 + m + m²)]

Solution:

a³ – b³ = (a − b) (a² + ab + b²)

1 – m² = (1 − m) (1+ m + m²)

10. One factor of x³+y³ is

(A) (x – y)

(B) (x + y)

(C) (x + y)³

(D) (x – y)³

[Answer: (B) (x + y)]

a³ + b³ = (a + b) (a² − ab + b²)

x³ + y³ = (x + y) (x² − xy + y²) 

Answer:

Exercise 3.4

1. (i ) 6 y (3 x − 2z) (ii) 3 x²y(3x³ y² + 2xy − 6) (iii) (b − 2c )( x + y)

(iv) ( x + y)( a + b) ( v ) ( 4 x − 1)( 2 x² −1) ( vi) ( x − 2)[3 y(x − 2) + 2]

(vii ) 2y(9x − 2 y − zx) ( viii) ( a − 3) ( a² +1) (ix) 3y ( y + 4)( y − 4) (x) (b − 1)(ab − c² )

2. (i ) (x + 7)² (ii) ( y − 5)² (iii ) ( c + 2)( c − 6) (iv) ( m + 9)( m − 8) (v) ( 2 x − 3)( 2 x −1)

3. (i) (4x + 3)³ (ii) (3p + 2q)³

4. (i) ( y − 6)³ (ii) ( 2 m − 5n)³

5. (D) 3x, (3x+2y)

6. (C) (2+m)(2–m)

7. (D) x²–x–20

8. (B) 3

9. (C) (1–m)(1+m+m²)

10. (B) (x+y)