Exercise 3.2 (Division of Algebraic Expressions)

Exercise 3.2

1. Fill in the blanks:

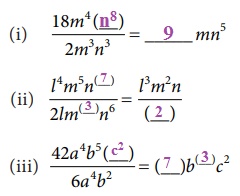
(i) [ 18m⁴ (n⁸) ] / [ 2m⁽³⁾n³ ] = 9 mn⁵ ]

(ii) [l⁴m⁵n⁽⁷⁾] / [2lm⁽³⁾n⁶] = [l³m²n] / 2 ]

(iii) [ 42a⁴b⁵ (c²) ] / [ 6(a)⁴(b)² ] = (7) b³ c² ]

2. Say True or False

(i) 8x ³ y ÷ 4x² = 2xy [Answer: True]

(ii) 7ab ³ ÷ 14ab = 2b² [Answer: False]

3. Divide

(i) 27 y³ by 3y

(ii) x³ y² by x²y

(iii) 45x³ y²z⁴ by (−15xyz)

(iv) (3xy)² by 9xy

Solution:

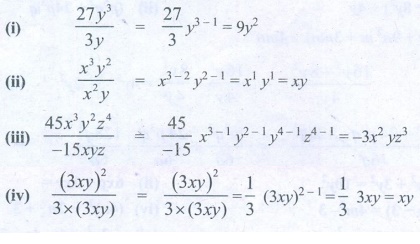
(i) 27y³ / 3y = (27/3) y³⁻¹ = 9y²

(ii) x³y² / x²y = x³⁻² y²⁻¹ = x¹y¹ = xy

(iii) [ 45x³ y²z⁴  ] / [−15xyz] = (45/−15) x³⁻¹ y²⁻¹ y⁴⁻¹z⁴⁻¹ = −3x² yz³

(iv) (3xy)² / [ 3 × (3xy) ] = [ (3xy)² ] / [3 × (3xy)] = (1/3) (3xy)²⁻¹ = (1/3) 3xy = xy

4. Simplify

Solution:

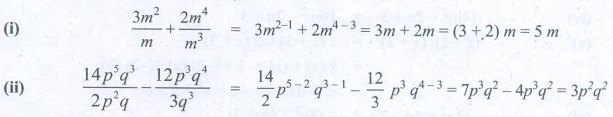
(i) [3m² / m ] + [2 m⁴ / m³ ] = 3m²⁻¹ + 2 m⁴⁻³ = 3m + 2m = (3 + 2) m = 5m

(ii) [ 14p⁵q³ / 2p²q ] – [ 12p³q⁴ / 3q² ] = [ (14/2) p⁵⁻²q³⁻¹ ] – [ 12/3 p³q⁴⁻³ ] = 7p³q² − 4p³q² = 3p²q²

5. Divide

(i) (32 y² − 8 yz) by 2y

(ii) (4m²n³ + 16m⁴ n² − mn) by 2mn

(iii) 5xy² - 18x² y³ + 6xy by 6xy

(iv) 81( p⁴ q²r³ + 2 p³q³ r² − 5p² q²r² ) by ( 3pqr)²

Solution:

(i) (32y² – 8yz) by 2y

[ 32y² – 8yz ] / 2y = [32y² / 2y ] – [ 8yz / 2y ] = (32/2) y²⁻¹ – (8/2) y¹⁻¹z = 16y – 4z

(ii) (4m² n³ + 16 m⁴ n² − mn) by 2 mn

[ 4m²n³ + 16m⁴n² – mn ] / 2mn = [4m²n³ / 2mn ] + [ 16m⁴n² / 2mn ] – [ mn / 2mn]

= (4/2)m²⁻¹ n³⁻¹  + (16/2)m⁴⁻¹ n²⁻¹ – (1/2)m¹⁻¹n¹⁻¹

= 2m¹n²  + 8 m³n¹ – (1/2)m⁰n⁰

= 2mn²  + 8m³n – 1/2

(iii) 5xy² − 18x²y³ + 6xy by 6xy

[ 5xy² − 18x²y³ + 6xy ] / 6xy = [ xy(5y − 18xy² + 6) ] / 6xy

= [ 5y − 18xy² + 6 ] / 6 = (5/6) y − 3xy² + 1

(iv) 81 (p⁴q²r³ + 2p³q³r² − 5p²q²r²) by (3pqr)²

[ 81 (p⁴q²r³ + 2p³q³r² − 5p²q²r²) ] / (3pqr)²

= [ 81 (p²q²r²) (p²r + 2pq− 5) ] / [ 9(p²q²r²) ]

= 81/9 (p²q²r²)¹⁻¹ (p²r + 2pq− 5)

= 9(p²r + 2pq− 5) = 9p²r + 18pq − 45

6. Identify the errors and correct them

(i) 7 y ² − y² +3y ² = 10 y²

(ii) 6xy + 3xy = 9x ² y²

(iii) m(4m − 3) = 4m² – 3

(iv) (4n)²− 2n + 3 = 4n ² − 2n + 3

(v) (x − 2)(x + 3) = x² – 6

(vi) -3p² + 4p - 7 = - (3p² + 4p - 7)

Solution:

(i) 7y^{2 −} y² + 3y² =  (7 – 1 + 3) y²  = (6 + 3) y² = 9y²

(ii) 6xy + 3xy =  (6 + 3) xy = 9xy

(iii) m (4m − 3) = m (4m) + m (−3) = 4m² − 3m

(iv) (4n)² − 2n + 3 = 16n² − 2n + 3

(v) (x − 2) (x + 3) = x (x + 3) − 2 (x + 3)

 = x(x) + (x) × 3 + (−2) (x) + (−2) (3)

 = x² + 3x − 2x − 6 = x² + x − 6

(vi) − 3p² + 4p − 7 = − (3p² − 4p +7)

7. Statement A: If 24p²q is divided by 3pq, then the quotient is 8p.

Statement B: Simplification of (5 x + 5) / 5 is 5x

(i) Both A and B are true

(ii) A is true but B is false

(iii) A is false but B is true

(iv) Both A and B are false

[Answer: (ii) A is true but B is false]

Solution:

[24p²q] / [3pq] = 8p² / p = 8p²⁻¹ = 8p

( [5x + 5] / 5 ) = [ 5(x + 1) ] / 5 =   x + 1

8. Statement A: 4x ² + 3x -2 = 2(2x² + 3x/2 -1)

Statement B: (2m–5)–(5–2m) = (2m–5) + (2m–5)

(i) Both A and B are true

(ii) A is true but B is false

(iii) A is false but B is true

(iv) Both A and B are false

[Answer: (i) Both A and B are true]

Solution:

(2m − 5) − (5 − 2m) = 2m − 5 − 5 + 2m = 4m − 10

(2m − 5) + (2m − 5) = 4m − 10

Answer:

Exercise 3.2

1.  

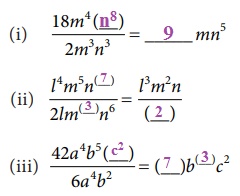
2. (i) True (ii) False

3. (i ) 9 y² (ii) xy (iii ) − 3x²yz³ (iv) x y

4. (i) 5m (ii) 3p³q²

5. (i ) 16 y − 4z (ii) 2 mn² + 8m³ n – 1/2 (iii ) (5/6)y - 3 xy² + 1 (iv) = 9 p²r +18pq – 45

6. (i ) 9 y² (ii) 9 xy (iii ) 4 m² −3m (iv) 16 n² − 2n + 3 (v) x² + 1x − 6 (vi) –(3p² –4p + 7)

7. (ii) A is true but B is false 

8. (i) both A and B are true