Application of Cubic Identities

Application of Cubic Identities

I. Using the identity (a + b)³ = a ³ + 3a² b + 3ab ² + b³

Example 3.13

Expand (x + 4)³

Solution:

Comparing (x + 4)³ with (a + b)³ , we get a = x , b = 4

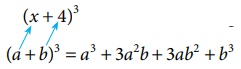
We know (a + b)³ = a ³ + 3a²b + 3ab ² + b³

(x + 4)³ = (x)³ + 3(x )² (4) + 3(x)(4)² + (4)³ (replacing a, b values)

= ( x )³ + 3x² (4) + 3(x)(16) + 64

(x + 4)³ = x³ + 12x ² + 48x + 64

(4)² = 4 × 4 = 16

(4)³ = 4 × 4 ×4=64

Try to expand this by using

(a + b)³ = a³ + b³ + 3ab(a + b)

Example 3.14

Find the value of (103)³

Solution:

Now, (103)³ = (100 + 3)³

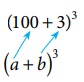
Comparing this with ( a + b)³ , we get a = 100 , b = 3

(a + b)³ = a ³ + 3a²b + 3ab² + b³ replacing a, b values,

(100 + 3)³ = (100)³ + 3(100)² (3) + 3(100)(3)² + (3)³

= 1000000+ 3(10000)(3) + 3(100)(9) + 27

= 1000000+ 90000 + 2700 + 27

(103)³ =1092727

II. Using the identity (a - b)³ = a ³ - 3a² b + 3ab ² - b³

Example 3.15

Expand: ( y − 5)³

Solution:

Comparing ( y − 5)³ with (a − b)³ , we get a = y , b = 5

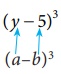
(a–b)³ = a³ − 3a²b + 3ab² − b³

(y –5)³ = ( y)³ – 3( y)² (5) + 3( y)(5)² - (5)³

 = ( y)³ – 3y² (5) + 3( y)(25) – 125

(y–5)³ = y³ −15y² + 75y −125

Try to expand this by using

(a − b)³ = a³ − b³ − 3ab(a − b)

Example 3.16

Find the value of (98)³

Solution:

Now, (98)³ = (100 − 2)³

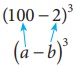
Comparing this with ( a − b)³ , we get a = 100 , b = 2

(a − b)³ = a³ − 3a²b + 3ab² − b³

(100 − 2)³ = (100)³ − 3(100)² (2) + 3(100)(2)² – (2)³

= 1000000 − 3(10000)(2) + 3(100)(4) – 8

= 1000000 − 60000 +1200 – 8

(98)³ = 941192

III. Using the identity (x + a)(x + b )(x + c) = x³ +(a + b + c)x² +(ab + bc + ca )x + abc

Example 3.17

Expand: (x + 3)(x + 5)(x + 2)

Solution:

Given

(x + 3)(x + 5)(x + 2)

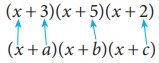
Comparing this with (x + a)(x + b)(x + c) , we get x = x , a = 3 , b = 5 , c = 2

(x + a)(x + b)(x + c) = x ³ + (a + b + c)x ² + (ab + bc + ca )x + abc

(x + 3)(x + 5)(x + 2) = ( x )³ + (3 + 5 + 2)(x)² + (3 × 5 + 5 × 2 + 2 × 3)x + (3)(5)(2)

= x ³ + 10x² + (15 + 10 + 6)x + 30

(x + 3)(x + 5)(x + 2) = x³ + 10x² + 31x + 30

Try these

Expand : (i) ( x + 5)³ (ii) ( y − 2)³ (iii) (x + 1)(x + 4)(x + 6)

Solution:

(i) Comparing (x + 5)³ with (a + b)³, we have a = x and b = 4.

(a + b)³ = a³ + 3a² b + 3ab² + b³

(x + 5)³ = x³ + 3x² (5) + 3 (x) (5)² + 5³

. = x³ + 15x² + 75x + 125

(ii) Comparing (y − 2)³ with (a − b)³ we have a = y b = z

(a − b)³ = a³ − 3a² b + 3ab² − b³

(y − 2)² = y³ – 3y²(2) + 3y(2)² + 2³

= y³ − 6y² + 12y + 8 

(iii) Comparing (x + 1) (x + 4) (x + 6) with (x + a) (x + b) (x + c) we have

a = 1 b =  4 and c = 6

(x + a) (x + b) (x + c) = x³ + (a + b + c) x² + (ab + bc + ca) x + abc

= x³ + (1 + 4 + 6) x² + ((1) (4) + (4) (6) + (6) (l))x + (1) (4) (6)

= x³ + 11x² + (4 + 24 + 6) x +24

= x³ + 11x² + 34x + 24