Exercise 3.5

Exercise 3.5

Miscellaneous Practice Problems

1. Subtract: −2(xy)² ( y ³ + 7x² y + 5) from 5y ² (x² y ³ − 2x⁴ y + 10x² )

Solution:

5y² (x² y³ − 2x⁴y + 10x²) − [(−2) (xy)² (y³ + 7x²y + 5)]

= [5y² (x² y³) − 5y² (2x⁴ y) + 5y² (10x²)] − [(−2) x²y² (y³ + 7x² y + 5)]

= (5y⁵x² − 10 x⁴y³ + 50 x²y²) − [(−2x²y²) (y³) + (−2x²y²) (7x²y) + (−2x²y²) (5)]

= 5x²y⁵ − 10x⁴y³ + 50x²y² − [−2x² y⁵ − 14x⁴y³ − 10x²y²]

= 5x²y⁵ − 10x⁴y³ + 50x²y² + 2x² y⁵ + 14x⁴y³ + 10x²y²

= (5 + 2) x²y⁵ + (−10 + 14) x⁴y³ + (+50 + 10)x²y²

= 7x²y⁵ + 4x⁴y³ + 60x²y²

2. Multiply ( 4x² + 9) and ( 3x − 2)

Solution:

(4x² + 9) (3x − 2) = 4x² (3x − 2) + 9 (3x − 2)

= (4x²) (3x) − (4x²) (2) + 9 (3x) − 9(2) = (4 × 3 × x × x²) − (4 × 2 × x²) + (9 × 3 × x) − 18

= 12x³ − 8x² + 27x − 18 (4x³ + 9) (3x− 2) = 12x³ − 8x² + 27x − 18 

3. Find the simple interest on Rs. 5a ²b² for 4ab years at 7b% per annum.

Solution:

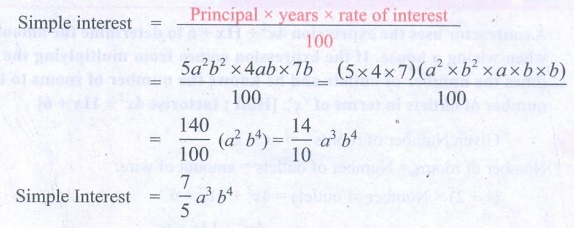
 Simple interest = [ Principal × years ×  rate of interest ] / 100

= [ 5a²b² × 4ab × 7b ] / 100 = [ (5 × 4 × 7) (a² × b² × a × b × b) ] / 100

= (140/100) (a³ b⁴) = (14/10)  a³ b⁴

Simple Interest = (7/5) a³ b⁴

4. The cost of a note book is Rs. 10ab. If Babu has Rs. ( 5a ²b + 20ab ² + 40ab) . Then how many note books can he buy?

Solution:

For ₹10 ab the number of note books can buy = 1.

For ₹ (5a²b + 20ab² + 40 ab) the number of note books can buy = Total amount / cost of 1 note book

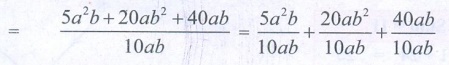
= [ 5a²b + 20ab² + 40ab ] / 10 ab = [ 5a²b / 10ab ] + [ 20ab² / 10ab ] + [ 40ab / 10ab ]

= 1/2 [  a²⁻¹ b¹⁻¹ ] + [ 2 a¹⁻¹ b²⁻¹ ] + [ 4 a¹⁻¹ b¹⁻¹ ] = (1/2)a¹ b⁰ + 2 a⁰ b¹ + 4 a⁰ b⁰

Number of note books he can buy = (½)a + 2b + 4

5. Factorise : ( 7y² − 19y − 6)

Solution:

7y² − 19y – 6 is of the form ax² + bx + c where a = 7; b = −19; c = − 6

Product = −42 : Sum = −19

1 × −42 = −42 : 1 + (−42) = −41

2 × −21 = −42 : 2 + (−21) = −19

The product a × c = 7x − 6 = − 42

sum b = −19

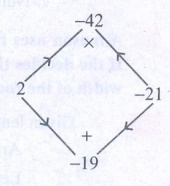
The middle term − 19y can be written as − 21y + 2y

7y² − 19y − 6 = 7y² − 21y + 2y − 6

= 7y (y − 3) + 2 (y − 3) = (y − 3) (7y + 2)

7y^{2 −} 19y − 6 = (y − 3) (7y + 2)

Challenging problems

6. A contractor uses the expression 4x² + 11x + 6 to determine the amount of wire to order when wiring a house. If the expression comes from multiplying the number of rooms times the number of outlets and he knows the number of rooms to be ( x + 2), find the number of outlets in terms of ‘x’. [Hint : factorise 4x ² + 11x + 6 ]

Solution:

Given Number of rooms = x + 2

Number of rooms × Number of outlets = amount of wire.

(x + 2) × Number of outlets = 4x² + 11x + 6

Number of outlets = [ 4x² + 11x + 6 ] / [ x + 2]         ...(1)

Now factorising 4x² + 11x + 6 which is of the form ax² + bx + c with a = 4 b = 11 c = 6.

The product a × c = 4 × 6 = 24

sum b = 11

Product = 24 : Sum = 11

1 × 24 = 24    : 1 + 24 = 25

2 × 12 = 24    :  2 + 12 = 14

3 × 8 = 24      :  3 + 8 = 11

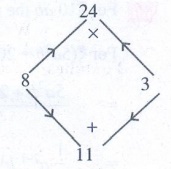
The middle term 11x can be written as 8x + 3x

∴ 4x² + 11x + 6 = 4x² + 8x + 3x + 6

= 4x (x + 2) + 3 (x + 2)

4x² + 11x + 6 = (x + 2) (4x + 3)

Now from (1) the number of outlets

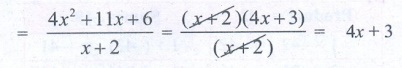
 [ 4x² + 11x + 6 ] / [ x + 2] = [ (x + 2) (4x + 3)] / (x + 2)    = 4x + 3

∴  Number of outlets = 4x + 3

7. A mason uses the expression x² + 6x + 8 to represent the area of the floor of a room. If the decides that the length of the room will be represented by ( x + 4) , what will the width of the room be in terms of x ?

Solution:

Given length of the room = x + 4

Area of the room = x² + 6x + 8 = x² + 6x + 8

Length × breadth = x² + 6x + 8

Breadth = [ x² + 6x + 8 ] / [ x + 4 ]      ……(1)

Factorizing x² + 6x + 8, it is in the form of ax² + bx + c

Where a = 1 ; b = 6 ; c = 8;

The product a × c = 1 × 8 = 8

Sum = 6

Product = 8 : Sum = 6

1 × 8 = 8   :  1 + 8 = 9

2 × 4 = 8   :  2 + 4 = 6

The middle term 6x can be written as 2x + 4x

∴ x² + 6x + 8 = x² + 2x + 4x + 8

= x (x + 2) + 4 (x + 2)

x² + 6x + 8 = (x + 2) (x + 4)

Now from (1)

breadth = [ x² + 6x + 8 ] / (x + 4) = [ (x + 2) (x + 4) ] / (x + 4) = (x + 2)

∴  Width of the room = x + 2

8. Find the missing term: y² + (…) x + 56 = (y+7)(y+..)

Solution:

We have (x + a) (x + b) = x² + (a + b)x + ab

56 = 7 × 8

∴  y² + (7 + 8)x + 56 = (y + 7) (y + 8)

9. Factorise : 16 p⁴ −1

Solution:

16p⁴ − 1 = 2⁴ p⁴ − 1 = (2²)² (p²)² − 1²

= (2²p²)² − 1²

Comparing with a² − b² = (a + b) (a − b) where a = 2² p² and b = 1

∴  (2²p²)² − 1² = (2²p² + 1) (2²p² − 1)

= (4p² + 1) (4p² − 1)

∴ 16p⁴ − l = (4p² + 1) (4p² − 1) = (4p² + 1) (2²p^{2 −} 1²)

= (4p² + 1) [(2p)² − 1²] = (4p² + 1) (2p + l) (2p − 1)

[ ∵ using a² − b² = (a + b) (a − b)]

∴ 16p⁴ − 1 = (4p² + 1) (2p + l) (2p − 1)

10. Factorise : 3x³ – 45x²y + 225xy² – 375y³

= 3x³ − 45x²y + 225xy² − 375y³

= 3(x³ − 15x²y + 75xy² − 125y³)

= 3(x³ − 3x²(5y) + 3x(5y)² − (5y)³)

= 3(x − 5y)³

Exercise 3.5

Miscellaneous Practice Problems

1. 7x²y⁵ + 4 x⁴y³ + 60x² y²

2.12 x³ − 8x² + 27x −18

3. S.I = 7/5 a³b⁴

4. 1/2 a + 2b + 4

5. ( y − 3)(7y + 2)

Challenging Problems

6. 4x + 3  

7. x + 2  

8. ( y + 7)( y + 8)  

9. (4 p² + 1)( 2p +1)(2p −1)  

10. 3( x − 5y)³