Questions with Answers, Solution | Measurements | Chapter 2 | 8th Maths - Try these, Student Activities, Think and answer | 8th Maths : Chapter 2 : Measurements
Chapter: 8th Maths : Chapter 2 : Measurements
Try these, Student Activities, Think and answer
Think
1. 22/7 and 3.14 are rational numbers. Is ‘π’ a rational number? Why?
Solution:
22/7 and 3.14 are rational numbers π has non−terminating and non−repoating decimal expansion. So it is not a rational number. It is an irrational number.
2. When is the ‘ π ’ day celebrated? Why?
Solution:
March 14th is the π day celebrated for every year. Approximately value of ‘π’ is 3.14.
Think
The given circular figure is divided into six equal parts. Can we call the equal parts as sectors? Why?

Answer:
No, the equal parts are not sectors. Because a sector is a plane surface that is enclosed between two radii and the circular arc of the circle.
Here the boundaries are not radii.
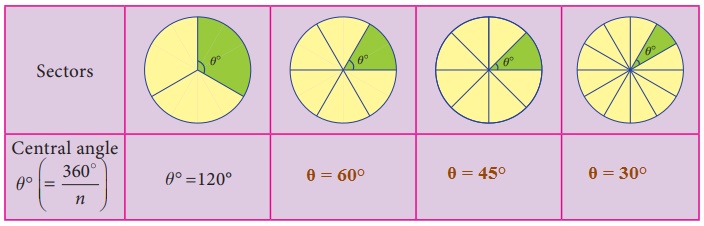
Try these
Fill the central angle of the shaded sector (each circle is divided into equal sectors)
Think
Instead of multiplying by 1/2, 1/3 and 1/4 , we shall multiply by 180°/360°, 120°/360° and 90°/360° respectively. Why?
Solution:
So, 180°/ 360° = 1/2
120°/360° = 1/3
90°/360° = 1/4
Think
If the radius of a circle is doubled, what will happen to the area of the new circle so formed?
Solution:
If r = 2r1
⇒ Area of the circle = πr2 = π (2r1)2 = π4r12 = 4πr12
Area = 4 × old area.
Think
All the sides of a rhombus are equal. Is it a regular polygon?
Solution:
For a regular polygon all sides and all the angles must be equal. But in a rhombus all the sides are equal. But all the angles are not equal
∴ It is not a regular polygon.
Try these
In the above example split the given mat into two trapeziums and verify your answer.
Solution:
Area of the mat = Area of I trapezium + Area of II trapezium
= [ 1/2 × h1 × (a1 + b1 )] + [ 1/2 × h2 × (a2 + b2 )] sq. units
= [ 1/2 × 2 × (7 + 5)] + 1/2 × 2 × (9 + 7) sq. feet
= 12 + 16 = 28 sq.feet
∴ Cost per sq.feet = ₹ 20
Cost for 28 sq. feet = ₹20 × 28 = ₹560
∴ Total cost for the entire mat = ₹560
Both the answers are the same.
Try these
Tabulate the number of faces (F), vertices (V) and edges (E) for the following polyhedrons. Also find F+V–E
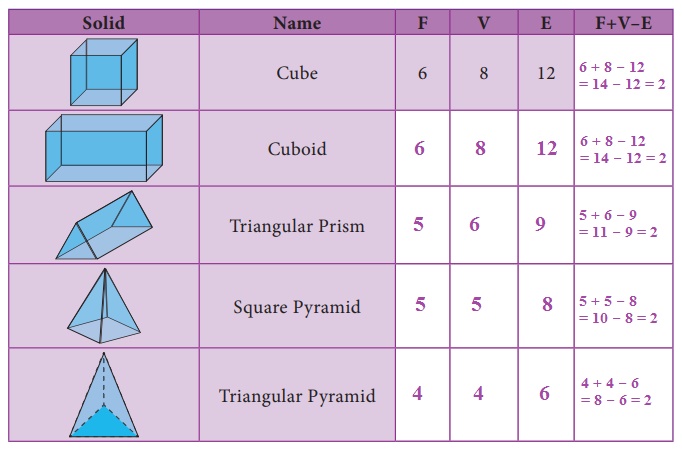
What do you observe from the above table? We observe that, F+V–E = 2 in all the cases. This is true for any polyhedron and this relation F+V–E = 2 is known as Euler’s formula.
From the table F + V – E = 2 for all the solid shapes.
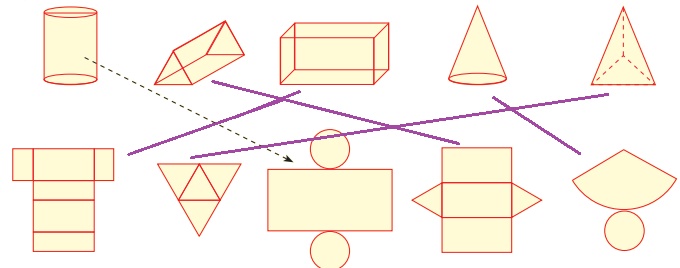
Activity
Draw a line to match the following shapes to their relevant nets.
Activity
1. Draw each of the given solid figures on an isometric dot sheet

2. Draw each of the given solid figures on a grid paper
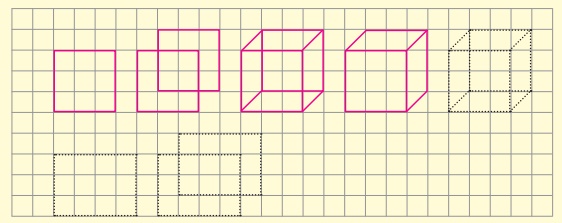
Activity
Draw and name the two dimensional shapes (2-D) which you get in the cross section of the following solid shapes.
Activity
• Using a bangle, draw a circle on the paper and cut it. Then mark any two points A and B on it and fold the circle so that the fold has A and B on it. Now, this line segment represents a chord.
• By paper folding, find two diameters and hence the centre of a circle.
• Check whether the diameter of a circle is twice its radius.
Note
The circumference of a circle is 2πr units, which can also be written as πd units. As π =3.14 (approximately) and it is slightly more than 3, for some quick guess, we shall say that a circle whose diameter is d units shall have its circumference slightly more than three times its diameter.
For example,
If a round table of diameter of 3m is to be decorated by flower strings around it, it will require a little more than 9m of flower strings.

Note
The part which has a smaller arc is called as the ‘minor segment’ and the part which has a larger arc is called as the ‘major segment’.
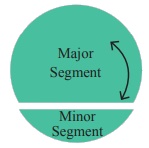
Note
1. If a circle of radius r units divided into n equal sectors, then the
Length of the arc of each of the sectors = [1/n] × 2πr units
and
Area of each of the sectors = [ 1/n ] × πr2 sq.units
2. Also, the area of the sector is derived as = [θº/360°] × πr2


Note
1. The perimeter of a semi-circle
P = l+2r units
= πr + 2r = (π + 2)r units
2. The perimeter of a circular quadrant
P = l + 2r = πr / 2 + 2r = ( π/2 + 2 ) r units
Do you Know:
1. The area of the unshaded regions in each of the squares of side a units are the same in all the cases given below.
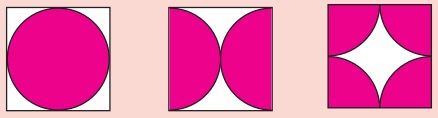
2. If the biggest circle is cut from a square of side ‘a’ units, then the remaining area in the square is approximately 3/14 a2 sq.units. ( π = 22/7)
3. The area of the biggest circle cut out from the square of ‘a’ units = 11/14 a2 sq. units (approximately)
4. In the given figure if π = 22/7 , the area of the unshaded part of a square of side a units is approximately 3/7 a2 sq.units and that of the shaded part is approximately 4/7 a2 sq.units.

Related Topics