Exercise 2.4

Exercise 2.4

Miscellaneous Practice Problems

1. Two gates are fitted at the entrance of a library. To open the gates easily, a wheel is fixed at 6 feet distance from the wall to which the gate is fixed. If one of the gates is opened to 90º, find the distance moved by the wheel (π = 3.14) .

Solution:

Let A be the position of the wall AC be the gate in initial position and AB be position when it is moved 90°.

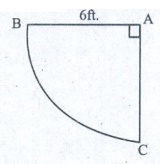
Now the arc length BC gives the distance moved by the wheel.

Length of the arc = [θ / 360°] × 2πr units

= [90° / 360°] × 2 × 3.14 × 6 feets

= 3.14 × 3 feets

= 9.42 feets

∴ Distance moved by the wheel = 9.42 feets.

2. With his usual speed, if a person covers a circular track of radius 150 m in 9 minutes, find the distance that he covers in 3 minutes (π = 3.14) .

Solution:

Radius of the circular track = 150m

Distance covers in 9 minutes = Perimeter of the circle = 2 ×  π × r units

Distance covered in 9 min = 2 × 3.14 × 150 m

∴ Distance covered in 1 min = [ 2 × 3.14 × 150 ] / 9 m

Distance covered in 3 min = [ 2 × 3.14 × 150 × 3 ] / 9  = 314 m

Distance he covers in 3 min = 314 m

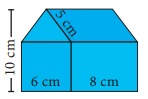
3. Find the area of the house drawing given in the figure.

Solution:

Area of the house = Area of a square of side 6 cm + Area of a rectangle with l = 8cm, b = 6 cm + Area of a Δ with b = 6 cm and h = 4 cm + Area of a parallelogram with b= 8 cm, h = 4 cm

= (side × side) + (l × b) + (1/2 × b × h) + bh cm² 

= (6 × 6) + ( 8 × 6) + (1/2 × 6 × 4) + (8 × 4) cm²

= 36 + 48 + 12 + 32 cm²

= 128 cm²

Required Area = 128 cm²

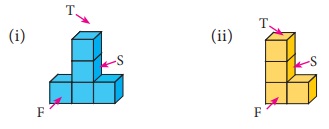
4. Draw the top, front and side view of the following solid shapes

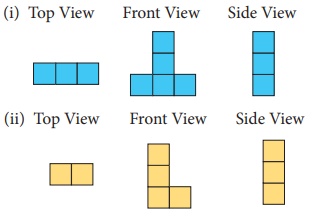
Solution: 

Challenging problems

5. Guna has fixed a single door of width 3 feet in his room where as Nathan has fixed a double door, each of width 1 1/2 feet in his room. From the closed position, if each of the single and double doors can open up to 120º, whose door takes a minimum area?

Solution:

(a)

Width of the door that Guna fixed = 3 feet.

When the door is open the radius of the sector = 3 feet

Angle covered = 120°

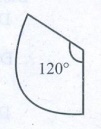
∴ Area required to open the door

= [120° / 360°] × πr² = [120° / 360°] × π × 3 × 3

= 3π feet²

(b)

Width of the double doors that Nathan fixed = 1 (½) feet.

Angle described to open = 120°

Area required to open = 2 × Area of the sector

= 2 × [120°/360°] × π × [3/2] × [3/2] feet² = 3π / 2 feet²

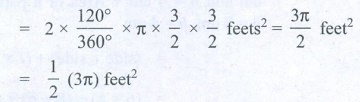
= (1/2 )(3π) feet²

∴ The double door requires the minimum area.

6. In a rectangular field which measures 15 m × 8m, cows are tied with a rope of length 3m at four corners of the field and also at the centre. Find the area of the field where no cows can graze. (π = 3.14)

Solution:

Area of the field where none of the cow can graze = Area of the rectangle − [Area of 4 quadrant circles] − Area of a circle

Area of the rectangle = l × b units²

= 15 × 8 m² = 120 m²

Area of 4 quadrant circles = 4 × (1/4) πr² units

Radius of the circle = 3m

Area of 4 quadrant circles = 4 × (1/4) × 3.14 × 3 × 3 = 28.26m²

Area of the circle at the middle = πr² units

= 3.14 × 3 × 3 m² = 28.26m²

∴  Area where none of the cows can graze

= [120 − 28.26 − 28.26]m² = 120 − 56.52 m² = 63.48m² (approx) 

7. Three identical coins each of diameter 6 cm are placed as shown. Find the area of the shaded region between the coins. (π = 3.14) ( √3 =1.732)

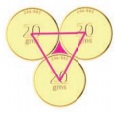
Solution:

Given diameter of the coins = 6 cm

∴  Radius of the coins = 6/2 = 3 cm

Area of the shaded region = Area of equilateral triangle − Area of 3 sectors of angle 60°

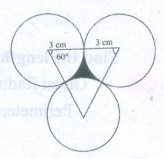
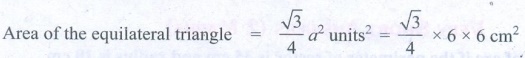
 Area of the equilateral triangle = √3/4 a² units² = √3/4 × 6 × 6 cm²

= [1.732 / 4] × 6 × 6 cm² = 15.588 cm²

Area of 3 sectors = 3 × [θ/360°] × [πr²] sq.units

= 3 × [60°/360°] × 3.14 × 3 × 3 cm² = 14.13 cm²

∴  Area of ther shaded region = 15.588 – 14.13 cm² = 1.458 cm²

Required area = 1.458 cm² (approximately) 

8. Using Euler’s formula, find the unknowns.

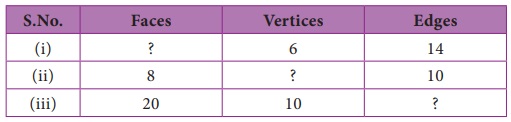
Solution:

Euler’s formula is given by F + V − E = 2

(i) V = 6, E = 14

By Euler’s formula = F + 6 − 14 = 2

F = 2 + 14 − 6

F = 10

(ii) F = 8, E = 10

By Euler’s formula = 8 + V − 10 = 2

V = 2 – 8 + 10

V = 4

(iii) F = 20, V = 10

By Euler’s formula = 20 + 10 − E = 2

30 − E = 2

E = 30 − 2

E = 28

Tabulating the required unknowns

Answer:

Exercise 2.4

Miscellaneous Practice Problems

1. 9.42 feet

2. 314 m

3. 128 cm²

4. 

Challenging Problems

5. double door requires the minimum area

6. 63.48 m² (approximately)

7. 1.46 cm² (approximately)

8. (i) F = 10 (ii) V = 4 (iii) E= 28