Combined shapes

Combined shapes

In our day-to-day life, we use infinitely many things with shapes like circle, triangle, square, rectangle, rhombus etc., don’t we? We use them separately as well as with two or three or more shapes combined together as shown in the following figures.

What do we observe from the above figures?

The shape of a glass window is like a semi-circle placed over a rectangle whereas the front – facing wall of a model house looks like a triangle over a square.

Likewise, list the shapes used to make an invitation card and a locker.

Thus, two or more plane figures joined with the sides of same measure give rise to combined shapes.

1. Perimeter of combined shapes

The perimeter of a combined shape is the sum of all the lengths of the sides that form a closed boundary.

For example, observe the Fig. 2.19 which has a square of side a units and an equilateral triangle of side a units combined together.

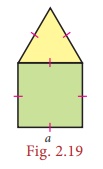
Though a square has 4 sides and an equilateral triangle has 3 sides, when they are combined together, we will have a total of only 5 sides as the boundary of the combined shape and not 7 sides. Isn’t it? So, the perimeter of the combined shape, here is 5a units.

2. Area of combined shapes

To find the area of a combined shape, split the combined shape into known simpler shapes, find their area separately and then add them up. That is, the area of combined shapes is nothing but the sum of all the areas of the simple shapes in it

To find the area of the Fig.2.20, find the area of the square and the area of the equilateral triangle separately and then add them up.

The combined shapes that we come across mostly in our day-to-day life are irregular polygons. To find the area of the given irregular polygon, we must identify the simple shapes in it, find their areas separately and then add them up.

For example, an irregular polygonal field given below can be split into known simpler shapes as under and then its area can be found.

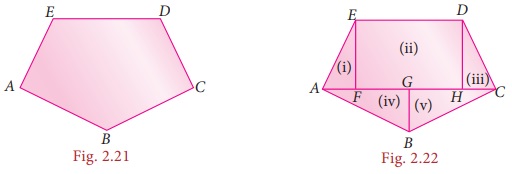
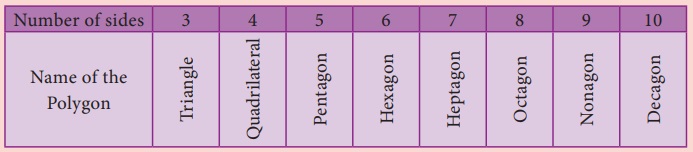
A closed plane figure formed by three or more sides is called a ‘polygon’ .Based on the es, some of the polygons are named as given below.

If all sides and all angles of a polygon are equal, then it is called as a regular polygon.

Examples: equilateral triangle, square etc., Other polygons are irregular polygons.

Examples: scalene triangle, rectangle etc.,

Think

All the sides of a rhombus are equal. Is it a regular polygon?

Solution:

For a regular polygon all sides and all the angles must be equal. But in a rhombus all the sides are equal. But all the angles are not equal

∴ It is not a regular polygon.

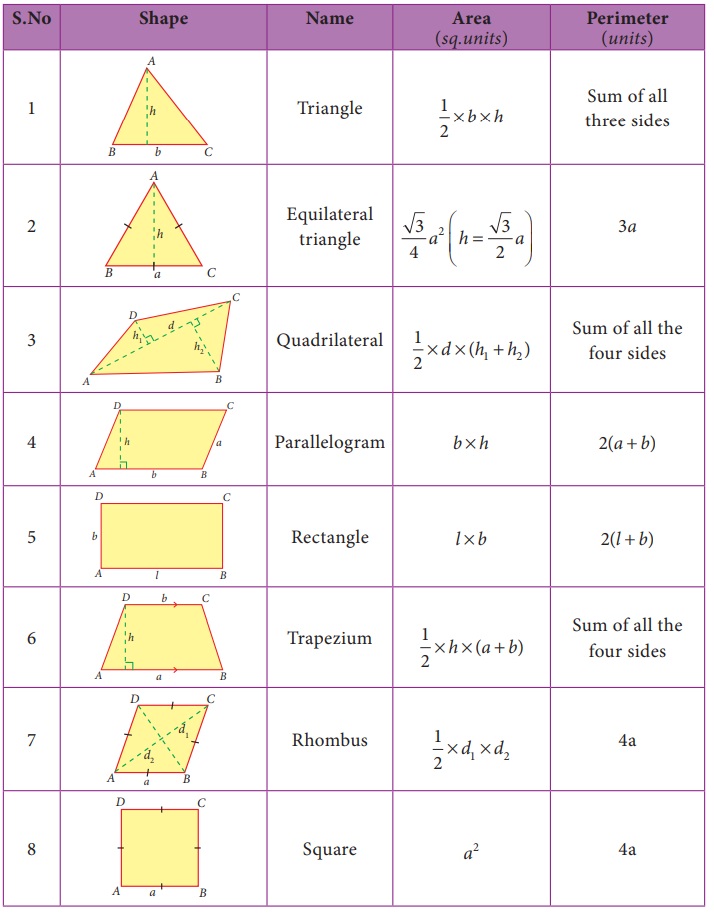
The formulae to find the area and the perimeter of some plane figures learnt in the earlier class are tabulated below and it will be helpful to find the area and the perimeter of combined figures.