Three dimensional (3-D) shapes

Three dimensional (3-D) shapes

Trace the outline of a ₹ 2 coin, ₹ 10 note and a square shaped biscuit on a paper.

What shapes have you traced? A circle, a rectangle and a square. Isn’t it? These shapes represents the plane figures. Also, these plane figures have two dimensions namely length and breadth. Now, you place some two rupee coins, some ten rupee notes and some square shaped biscuits respectively on the drawn shapes as shown in the figure.

What do you get now? A cylinder, a cuboid and a cube. Isn’t it? These shapes do not lie completely on the plane and they occupy some space also. That is, they have the third dimension namely the height along with the dimensions length and breadth. Thus, the shapes which have three dimensions namely length, breadth and height (depth) are called three dimensional shapes, simply called as 3-D shapes. Some examples of 3-D shapes are

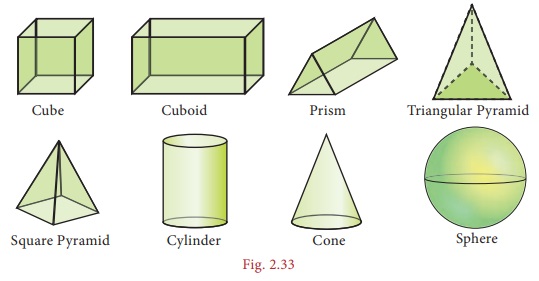
1. Faces, Edges and Vertices

Observe the following shape. What is it? A cube. A cube is made of six square shaped planes. These 6 square shaped planes of the cube are known as its faces.

A line segment which connects any two faces of a cube is called as Edge and each corner point where three edges meet is called as Vertex. So, a cube has 6 faces, 12 edges and 8 vertices.

Try these

Tabulate the number of faces (F), vertices (V) and edges (E) for the following polyhedrons. Also find F+V–E

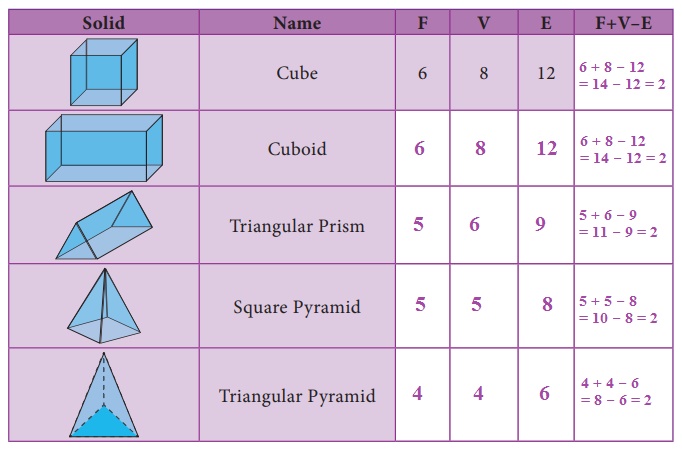
What do you observe from the above table? We observe that, F+V–E = 2 in all the cases. This is true for any polyhedron and this relation F+V–E = 2 is known as Euler’s formula.

From the table F + V – E = 2 for all the solid shapes.

2. Nets for building three dimensional (3-D) shapes

When we buy sweets, a shop keeper picks a fl at shaped card which has some flips and makes a rectangular shaped box (cuboid) by folding it as shown in the figure. Then, he arranges the sweets in the box and gives it to us

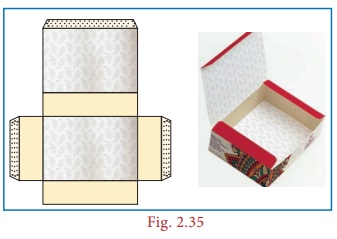
The flat shaped card already designed for making the box excluding flaps (dotted lines) is known as a net.

For example, from the following nets we can build cubes and square pyramids.

Activity

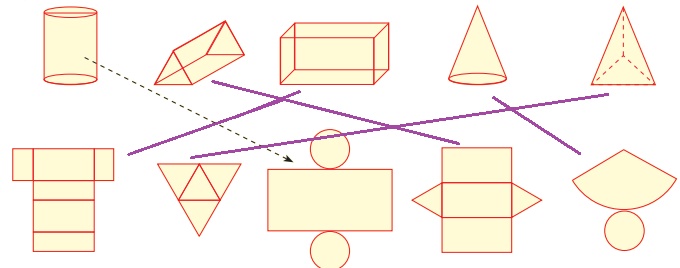
Draw a line to match the following shapes to their relevant nets.

3. Drawing 3-D shapes using isometric dot sheets and grid sheets

Activity

1. Draw each of the given solid figures on an isometric dot sheet

2. Draw each of the given solid figures on a grid paper

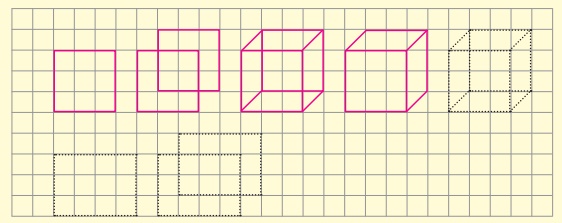
4. Cross section of solid shapes

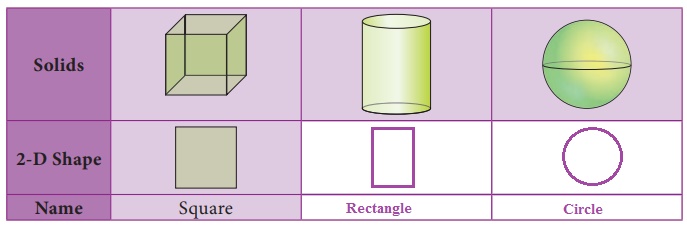
When we cut the vegetables in cross section for cooking purpose, we see some plane figures in it. For example, the cross section of a carrot and a plantain stem is a circle.

In the same way, we can see squares and rectangles in the cross section of a bread loaf and bricks etc.,

Activity

Draw and name the two dimensional shapes (2-D) which you get in the cross section of the following solid shapes.

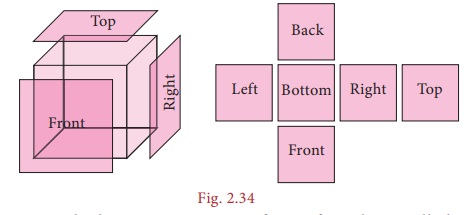
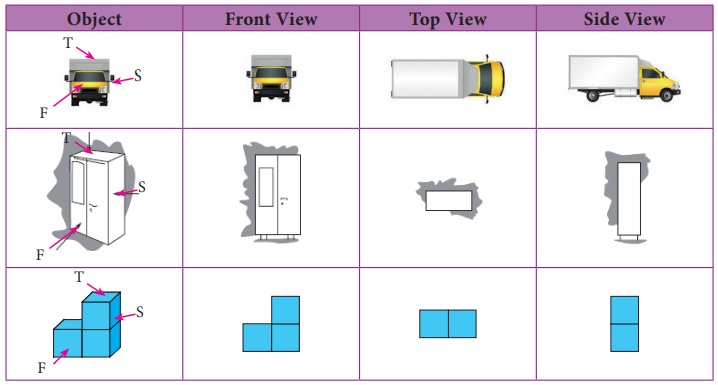
5. 3-D shapes in different views

A 3-D object may look different from different positions. View of a 3D shape is what you see while observing the object from different positions. Some of the views are front view, top view and side view. The different views of some of the objects are as shown below.