Parts of a Circle

Parts of a Circle

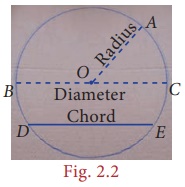
A circle is the path traced by a moving point so that its distance from a fixed point is always constant. The fixed point of the circle is called its ‘centre’ and the constant distance is called its ‘radius’.

Further, if any two points on a circle are joined by a line segment, then the line segment is called a ‘chord’. A chord divides a circle into two parts. A chord which passes through the centre of a circle is called as a ‘diameter’. A diameter of a circle divides it into two equal parts. It is also the ‘longest chord’ of a circle.

Activity

• Using a bangle, draw a circle on the paper and cut it. Then mark any two points A and B on it and fold the circle so that the fold has A and B on it. Now, this line segment represents a chord.

• By paper folding, find two diameters and hence the centre of a circle.

• Check whether the diameter of a circle is twice its radius.

1. Circular Arc and Circular Sector

Look at the glass bangle and the pizza given in Fig. 2.3 carefully.

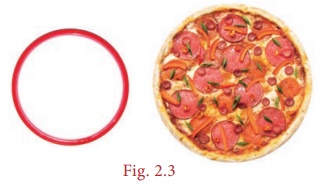
Though both are of circular shapes, what we understand is that, the bangle indicates the boundary of the circle, whereas the pizza indicates the plane enclosed within the boundary of the circle. Thus, it is clear that the bangle indicates the circumference of the circle whereas the pizza indicates the area of the circle.

From them, cut a part as shown in Fig. 2.4.

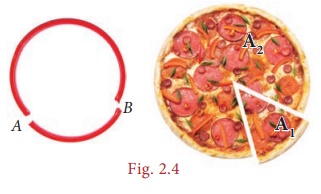
Each of the glass bangle pieces represents the circular arcs. Here, arc  is the smaller one and arc  is the larger one. Each of the parts of the pizza represents the circular sectors. Here A1 is the minor sector and A2 is the major sector.

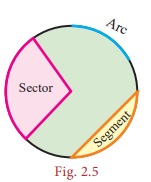
• A part of the circumference of a circle is called a circular arc.

• The plane surface that is enclosed between two radii and the circular arc of a circle is called a sector.

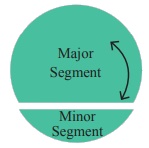
• Each part of a circle which is divided by a chord is called a segment.

Note

The part which has a smaller arc is called as the ‘minor segment’ and the part which has a larger arc is called as the ‘major segment’.

Think

The given circular figure is divided into six equal parts. Can we call the equal parts as sectors? Why?

Answer:

No, the equal parts are not sectors. Because a sector is a plane surface that is enclosed between two radii and the circular arc of the circle.

Here the boundaries are not radii.

Central Angle

The angle formed by a sector of a circle at its centre is called the central angle. The vertex of the central angle of the sector is the centre of the circle. The two arms of it are the radii. In the Fig. 2.7, the shaded sector uhas the central angle, ∟AOB = θº (read as theta) and its two arms OA and OB are the radii of the circle.

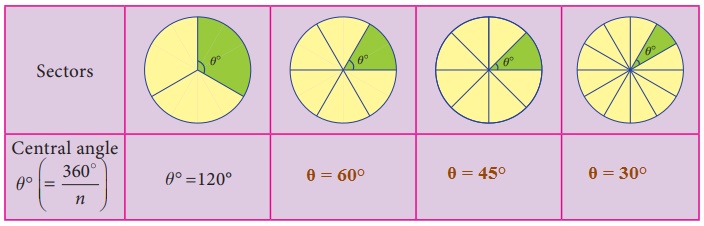
The central angle of a circle is 360°. If a circle is divided into ‘n’ equal sectors, the central angle of each of the sectors is θº = 360º/n.

For example, the central angle of a semicircle = 360º/2 = 180º and the central angle of a quadrant of a circle = 360º/4 = 90º

Try these

Fill the central angle of the shaded sector (each circle is divided into equal sectors)

2. Length of the arc and Area of the sector

We have already learnt that a circle of radius ‘r’ units has

Central angle = 360°

Circumference of the circle = 2πr units

Area of the circle =πr2 Sq.units.

First, let us take a circle . If a circle is divided into 2 equal sectors we will get 2 semi-circles. The length of a semi-circular arc is half of the circumference of the circle and the area of the semi-circle is half of the area of the circle.

What do we know from this?

If the ratio of the central angle of a sector to the central angle of a circle is multiplied with the circumference and the area of the circle, we can find the length of the arc of that sector and its area respectively.

That is, if we assume that the central angle of a sector of radius ‘r’ units as θ°, then, the ratio of the central angle θ° to 360° is θ°/360°.

Length of the arc, l = [ θº / 360º ] × 2πr units

Area of the sector, A = [ θº / 360º ] × πr2 sq.units.

Think

Instead of multiplying by 1/2, 1/3 and 1/4 , we shall multiply by 180°/360°, 120°/360° and 90°/360° respectively. Why?

Solution:

So, 180°/ 360° = 1/2

120°/360° = 1/3

90°/360° = 1/4

Note

1. If a circle of radius r units divided into n equal sectors, then the

Length of the arc of each of the sectors = [1/n] × 2πr units

and

Area of each of the sectors = [ 1/n ] × πr2 sq.units

2. Also, the area of the sector is derived as = [θº/360°] × πr2

3. Perimeter of a sector

We already know that the total length of the boundary of a closed part is its perimeter, Isn’t it? What is the boundary of a sector? Two radii (OA and OB) and an arc .

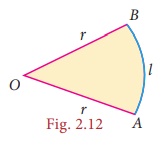
So, the perimeter of a sector = length of the arc + length of two radii

P = l + 2r units

Perimeter of a sector, P = l + 2r units

Tamil people always have a prominent role in the history of Mathematics. They had recorded in the form of a song on how to find the area of a circle, a few thousand years before itself, in the book titled ‘Kanakkathikaram’. (கணக்கதிகாரம்). The song is as follows:

“வட்டத்தரை கொண்டு விட்டத்தரை தாக்கச்

சட்டெனத் தோன்றும் குழி ”

Meaning:

‘வட்டத்தரை’ represents half of the circumference and ‘விட்டத்தரை’ represents half of the diameter which is the radius and ‘குழி’ represents the area. In this song, the Tamil people had recorded that, if half the circumference is multiplied by half the diameter, the area of the circle can be calculated

Area of the circle = வட்டத்தரை × விட்டத்தரை

= 1/2 of circumference × 1/2 of diameter = (1/2 × 2πr) × r

Area of the circle, A = πr2 sq.units

Note

1. The perimeter of a semi-circle

P = l+2r units

= πr + 2r = (π + 2)r units

2. The perimeter of a circular quadrant

P = l + 2r = πr / 2 + 2r = ( π/2 + 2 ) r units

The radius of a sector is 21cm and its central angle is 120°. Find (i) the length of the arc (ii) area of the sector (iii) perimeter of sector. ( π = 22/7)

Solution:

Aliter:

Area of the sector

 A = lr/2 sq.units

 = [44 × 21] / 2 = 462 cm2