Perimeter and Area of Combined shapes - Example solved problems

Example 2.5

Find the perimeter and area of the given Fig.2.23. (π = 22/7)

Solution:

Radius of a circular quadrant, r = 3.5 cm and side of a square, a = 3.5 cm.

The given figure is formed by the joining of 4 quadrants of a circle with each side of a square. The boundary of the given figure consists of 4 arcs and 4 radii.

(i) Perimeter of the given combined shape

= 4 × length of the arcs of the quadrant of a circle + 4 × radius

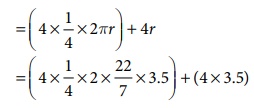
= 22 + 14 = 36 cm (approximately)

(ii) Area of the given combined shape

= area of the square + 4 × area of the quadrants of the circle

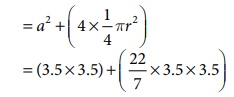
A = 12.25+38.5 = 50.75 cm² (approximately)

Example 2.6

Nishanth has a key-chain which is in the form of an equilateral triangle and a semicircle attached to a square of side 5 cm as shown in the Fig. 2.24. Find its area. ( π = 3.14, √3 = 1.732)

Solution:

Side of the square = 5 cm

Diameter of the semi-circle = 5 cm ⇒ Radius = 2.5 cm

Side of the equilateral triangle = 5 cm

∴ Area of the key-chain = area of the semi circle + area of the square + area of the equilateral triangle

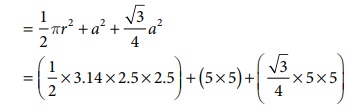
= 9.81+ 25 + 10.83

= 45.64 cm² (approximately)

Example 2.7

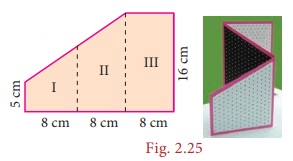
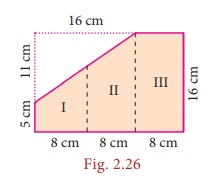
A 3-fold invitation card is given with measures as in the Fig. 2.25. Find its area.

Solution:

Figures I and II are trapeziums separately as well as combinedly.

The parallel sides of the combined trapezium (I and II) are 5 cm and 16 cm and its height, h = 8 + 8 = 16cm , length of the rectangle (III) = 16 cm and its breadth = 8 cm

Area of the combined invitation card = area of the combined trapezium + area of the rectangle

= 1/2 ×h×(a +b)+ l ×b

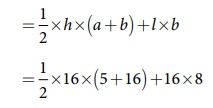
= 1/2×16×(5 +16)+16×8

= 168 + 128 = 296 cm²

Aliter:

Area of the invitation card = area of the outer rectangle – area of the right angled triangle

= [l ×b] – [ 1/2 ×b×h ]

= [ 24×16 ] – [ 1/2 ×11×16 ]

= 384 − 88 = 296 cm²

Example 2.8

Seenu wants to buy a floor mat for his kitchen at home as given in Fig. 2.27. If the cost of the mat is ₹ 20 per square foot, what will be the cost of the entire mat?

Solution:

The mat given in the figure can be split into two rectangles as follows:

Area of the entire mat = area of the I rectangle + area of the II rectangle

= l₁ ×b₁ + l₂ ×b₂

= 5 ×2 + 9 ×2 = 10 +18 =28 sq.feet

Cost per sq. foot = ₹ 20

The total cost of the entire mat = 28 × ₹ 20 = ₹ 560

Try these

In the above example split the given mat into two trapeziums and verify your answer.

Solution:

Area of the mat = Area of I trapezium + Area of II trapezium

= [ 1/2 × h₁ × (a₁ + b₁ )] + [ 1/2 × h₂ × (a₂ + b₂ )] sq. units

= [ 1/2  × 2 × (7 + 5)] + 1/2 × 2 × (9 + 7) sq. feet

= 12 + 16 = 28 sq.feet

∴ Cost per sq.feet =  ₹ 20

Cost for 28 sq. feet =  ₹20 × 28 = ₹560

∴ Total cost for the entire mat = ₹560

Both the answers are the same. 

Example 2.9

Find the area of the shaded region in the square of side 10 cm as given in the Fig. 2.29. (π = 22/7)

Solution:

Mark the unshaded parts of the given figure as I, II, III and IV

Area of the I and III parts = Area of the square – Area of 2 semicircles

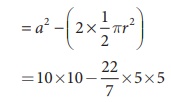
= 10×10 – 22/7 ×5×5 = 100 – 78.57 = 21.43 cm².

Similarly, the area of the II and IV parts = 21.43 cm²

Area of the unshaded parts (I, II, III and IV)

= 21.43 ×2 = 42.86 cm² (approximately)

Area of the shaded part = area of the square – area of the unshaded parts

= 100 – 42.86 = 57.14 cm² (approximately)

Do you Know:

1. The area of the unshaded regions in each of the squares of side a units are the same in all the cases given below.

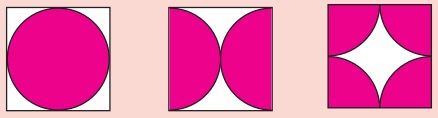
2. If the biggest circle is cut from a square of side ‘a’ units, then the remaining area in the square is approximately 3/14 a² sq.units. ( π = 22/7)

3. The area of the biggest circle cut out from the square of ‘a’ units = 11/14 a² sq. units (approximately)

4. In the given figure if π = 22/7 , the area of the unshaded part of a square of side a units is approximately 3/7 a² sq.units and that of the shaded part is approximately 4/7 a² sq.units.

Example 2.10

Find the area of an irregular polygon field whose measures are as given in the Fig. 2.30.

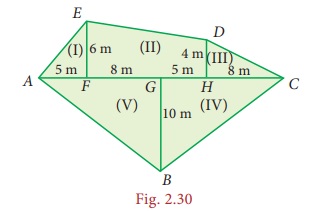
Solution:

The given field has four triangles (I, III, IV and V) and a trapezium (II).

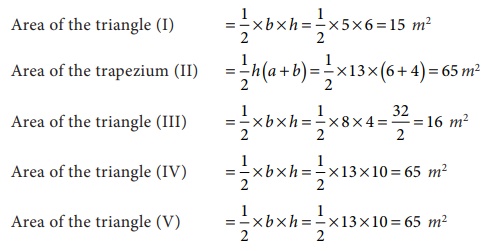
 ∴ The total area of the field = 15 + 65 + 16 + 65 + 65 = 226 m²