Parts of a Circle: Numerical Example solved problems

Example 2.1

A circular shaped gymnasium ring of radius 35cm is divided into 5 equal arcs shaded with different colours. Find the length of each of the arcs.

Solution:

Radius, r = 35 cm and n = 5.

Length of each of the arcs, l = 1/n × 2πr units

= 1/5 × 2 × π × 35 = 14 π cm.

Example 2.2

A spinner of radius 7.5 cm is divided into 6 equal sectors. Find the area of each of the sectors.

Solution:

Radius, r = 7.5 cm and n = 6.

Area of each of the sectors, A = 1/n × πr2 sq. units

= 1/6 × π × 7.5 × 7.5

= 9.375π sq. cm

Example 2.3

Kamalesh has a dining table, circular in shape of radius 70 cm whereas Tharun has a circular quadrant dining table of radius 140 cm. Whose dining table has a greater area? [π = 22/ 7]

Solution:

Area of the dining table with Kamalesh = πr2 sq. units

= 22/7 × 70 × 70

A = 15400 sq.cm (approximately.)

Area of the circular quadrant dining table with Tharun

= 1/4 πr2 = 1/4 × 22/7 ×140 ×140

 A = 15400 sq.cm (approximately.)

We find that, the area of the dining tables of both of them have the same area.

Think

If the radius of a circle is doubled, what will happen to the area of the new circle so formed?

Solution:

If r = 2r₁

⇒  Area of the circle = πr² = π (2r₁)² = π4r₁² = 4πr₁²

Area = 4 × old area.

Example 2.4

Four identical medals, each of diameter 7cm are placed as shown in Fig. 2.18. Find the area of the shaded region between the medals. [π = 22/7]

Solution:

Diameter, d = 7 cm, therefore r = 7/2 cm.

Area of the shaded region = Area of the square – 4 × Area of the circular quadrant

= a2 − 4 × 1/4 πr2

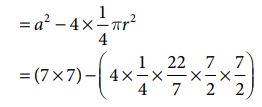
= (7×7) – ( 4 × 1/4 × 22/7 × 7/2 ×7/2 )

= 49 –38.5 = 10.5 sq.cm. (approximately)