Applications of Matrices: Solving System of Linear Equations - System of Linear Equations in Matrix Form | 12th Mathematics : UNIT 1 : Applications of Matrices and Determinants
Chapter: 12th Mathematics : UNIT 1 : Applications of Matrices and Determinants
System of Linear Equations in Matrix Form
System of Linear Equations in Matrix Form
A system of m linear equations in n unknowns is of
the following form:
a11x1 + a12x2 + a13x3
+ ŌĆ”ŌĆ”ŌĆ” + a1nxn + = b1
a21x1 + a22x2 + a23x3
+ ŌĆ”ŌĆ”ŌĆ” + a2nxn + = b2
a31x1 + a32x2 + a3x3
+ ŌĆ”ŌĆ”ŌĆ” + a3nxn + = b3
ŌĆ”.. ŌĆ”. ŌĆ”.. ŌĆ”.. ŌĆ”.. ...
Am1x1 + am2x2 + am3x3
+ ŌĆ”ŌĆ”ŌĆ” + amnxn + = bm
where the coefficients aij , i = 1, 2, ŌĆ”. , m; j = 1, 2,ŌĆ”.., n and bk , k = 1, 2,ŌĆ”.., m are constants. If all
the bk 's are zeros, then the above system is called a homogeneous system of linear equations. On
the other hand, if at least one of the bk 's is non-zero,
then the above system is called a non-homogeneous system of linear equations.
If there exist values ╬▒1 , ╬▒2 , ŌĆ”.. , ╬▒n for x1,
x2 , ŌĆ”. , xn respectively
which satisfy every equation of (1), then the ordered n ŌłÆ tuple (╬▒1 , ╬▒2 , ŌĆ”. , ╬▒n ) is called a solution of (1). The above system (1) can be put in a matrix form as
follows:
Let A =  be
the m x n matrix formed by the coefficients of x1, x2 , x3,ŌĆ”. , xn
. The first row of A is formed by the coefficients of x1, x2 , x3,ŌĆ”. , xn
in the same order in which they occur in the first equation. Likewise, the
other rows of A are formed. The first
column is formed by the coefficients of x1
in the m equations in the same order.
The other columns are formed in a similar way.
be
the m x n matrix formed by the coefficients of x1, x2 , x3,ŌĆ”. , xn
. The first row of A is formed by the coefficients of x1, x2 , x3,ŌĆ”. , xn
in the same order in which they occur in the first equation. Likewise, the
other rows of A are formed. The first
column is formed by the coefficients of x1
in the m equations in the same order.
The other columns are formed in a similar way.
Let X = ![]() be
the n x1 order column matrix formed
by the unknowns x1, x2
, x3,ŌĆ”. , xn
be
the n x1 order column matrix formed
by the unknowns x1, x2
, x3,ŌĆ”. , xn
Let B = ![]() be the m x 1 order column matrix
formed by the right-hand side constants b1,
b2 , b3 , ŌĆ”. , bm
.
be the m x 1 order column matrix
formed by the right-hand side constants b1,
b2 , b3 , ŌĆ”. , bm
.
Then we get

Then AX = B is a matrix equation involving matrices and it is
called the matrix form of the system of
linear equations (1). The matrix A is called the coefficient matrix of the system and the
matrix
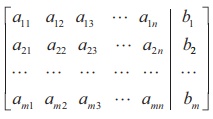
is called the augmented matrix of the system. We
denote the augmented matrix by [ A | B ].
As an example, the matrix form of the system of linear equations
2x + 3y - 5z + 7 = 0, 7 y + 2z - 3x = 17, 6x - 3y - 8z + 24 = 0
is 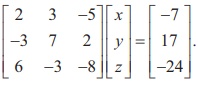
Related Topics