Matrices: Cramer’s Rule

Cramer’s Rule

This rule can be applied only when the coefficient matrix is a square matrix and non-singular. It is explained by considering the following system of equations:

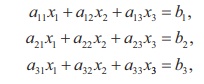
where the coefficient matrix 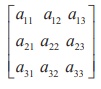 is non-singular. Then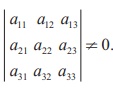 

Let us put Δ = . Then, we have

Note

Replacing the first column elements a₁₁ , a₂₁ , a₃₁ of Δ with b₁ , b₂ , b₃ respectively, we get Δ₁. Replacing the second column elements a₁₂ , a₂₂ , a₃₂ of Δ with b₁ , b₂ , b₃ respectively, we get Δ₂ . Replacing the third column elements a₁₃ , a₂₃ , a₃₃ of Δ with b₁ , b₂ , b₃ respectively, we get Δ₃.

If Δ = 0, Cramer’s rule cannot be applied.

Example 1.25

Solve, by Cramer’s rule, the system of equations

x₁ − x₂ = 3, 2x₁ + 3x₂ + 4x₃ = 17, x₂ + 2x₃ = 7.

Solution

First we evaluate the determinants

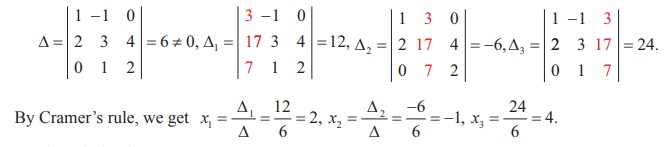
So, the solution is (x₁ = 2, x₂ = - 1,  x₃ = 4).

Example 1.26

In a T20 match, Chennai Super Kings needed just 6 runs to win with 1 ball left to go in the last over. The last ball was bowled and the batsman at the crease hit it high up. The ball traversed along a path in a vertical plane and the equation of the path is y = ax² + bx + c with respect to a xy -coordinate system in the  vertical  plane  and  the  ball  traversed   through   the   points  (10,8), (20,16), (30,18) , can you conclude that Chennai Super Kings won the match?

Justify your answer. (All distances are measured in metres and the meeting point of the plane of the path with the farthest boundary line is (70, 0).)

Solution

The path  y = ax2 + bx + c  passes through the points (10,8), (20,16), (40, 22) . So, we get the system of equations 100a + 10b + c = 8, 400a + 20b + c = 16,1600a + 40b + c = 22. To apply Cramer’s rule, we find

When x = 70, we get y = 6. So, the ball went by 6 metres high over the boundary line and it is impossible for a fielder standing even just before the boundary line to jump and catch the ball. Hence the ball went for a super six and the Chennai Super Kings won the match.