Definition, Formulas, Solved Example Problems - Matrix Inversion Method | 12th Mathematics : UNIT 1 : Applications of Matrices and Determinants
Chapter: 12th Mathematics : UNIT 1 : Applications of Matrices and Determinants
Matrix Inversion Method
Matrix Inversion Method
This method can be
applied only when the coefficient matrix is a square matrix and non-singular.
Consider the matrix equation
AX = B , ŌĆ” (1)
where A is a square matrix and non-singular. Since A is
non-singular, AŌłÆ1 exists and AŌłÆ1 A = AAŌłÆ1 = I. Pre-multiplying both sides of (1) by AŌłÆ1, we get AŌłÆ1 ( AX ) = AŌłÆ1B. That is, ( AŌłÆ1 A) X = AŌłÆ1B. Hence, we get X = AŌłÆ1B.
Example 1.22
Solve the following system of linear equations, using matrix
inversion method:
5x +
2 y = 3, 3x + 2 y = 5 .
Solution
The matrix form of the system is AX = B , where 
We find |A| = 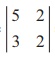 =
10 - 6= 4 ŌēĀ 0. So, AŌłÆ1 exists
and AŌłÆ1 =
=
10 - 6= 4 ŌēĀ 0. So, AŌłÆ1 exists
and AŌłÆ1 = 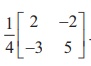
Then, applying the formula X = AŌłÆ1B , we get
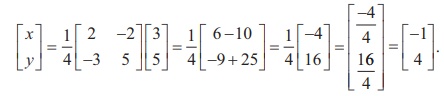
So the solution is (x =
ŌłÆ1, y = 4).
Example 1.23
Solve the following
system of equations, using matrix inversion method:
2x1 + 3x2
+ 3x3 = 5,
x1 ŌĆō 2x2 + x3 = -4,
3x1 ŌĆō x2 ŌĆō 2x3 = 3
Solution
The matrix form of the system is AX = B,where
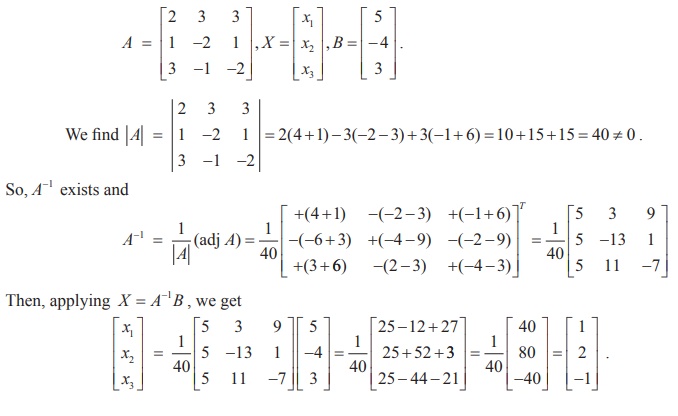
So,
the solution is ( x1 = 1, x2 = 2, x3 = ŌłÆ1) .
Example 1.24
If 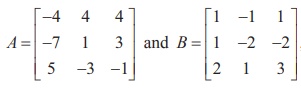 , find the
products AB and BA and hence solve the system of equations x ŌłÆ y + z = 4, x ŌĆō
2y ŌĆō 2z = 9, 2x + y +3z =1.
, find the
products AB and BA and hence solve the system of equations x ŌłÆ y + z = 4, x ŌĆō
2y ŌĆō 2z = 9, 2x + y +3z =1.
Solution
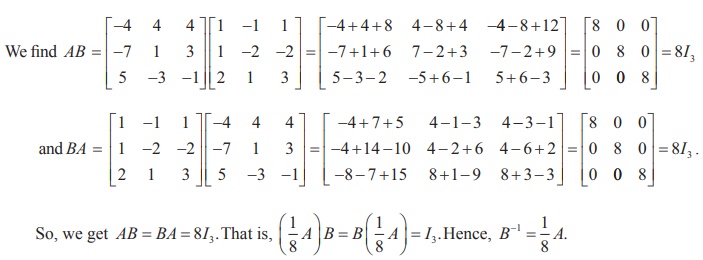
Writing
the given system of equations in matrix form, we get
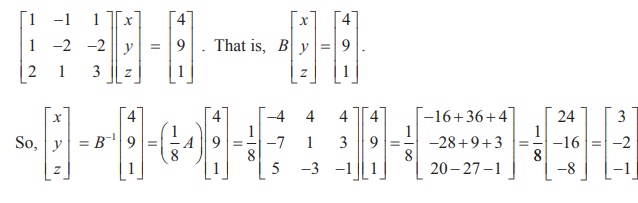
Hence, the solution is (x = 3, y = - 2, z = ŌłÆ1).
Related Topics