Definition, Theorem, Formulas, Solved Example Problems | Inverse of a Non-Singular Square Matrix - Application of matrices to Geometry | 12th Mathematics : UNIT 1 : Applications of Matrices and Determinants
Chapter: 12th Mathematics : UNIT 1 : Applications of Matrices and Determinants
Application of matrices to Geometry
Application of matrices to Geometry
There is a special type of non-singular matrices which are widely
used in applications of matrices to geometry. For simplicity, we consider
two-dimensional analytical geometry.
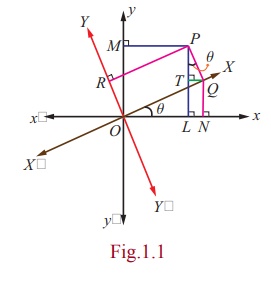
Let O be the origin, and x 'O x
and y 'Oy be the x -axis and y -axis.
Let P be a point in the plane whose coordinates are (x, y)
with respect to the coordinate system. Suppose that we rotate the x -axis and y
-axis about the origin, through an angle ╬Ė as shown in the figure. Let X 'OX and
Y 'OY be the new X -axis and new Y -axis. Let
( X ,Y ) be the new set of coordinates of P with
respect to the new coordinate system. Referring to
Fig.1.1, we get
x = OL = ON ŌłÆ LN = X cos ╬Ė ŌĆō QT = X cos ╬Ė ŌłÆ Y sin ╬Ė ,
y = PL = PT + TL = QN + PT =
X sin ╬Ė + Y cos ╬Ė .
These equations provide transformation of one coordinate system
into another coordinate system.
The above two equations can be written in the matrix form
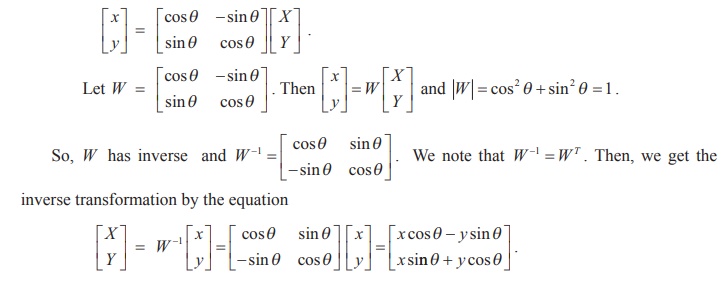
Hence, we get the
transformation X = x cos╬Ė
- y sin╬Ė , Y = x sin╬Ė
+ y cos╬Ė .
This transformation is
used in Computer
Graphics and determined by the matrix 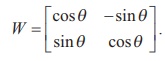
We note
that the matrix W satisfies a special
property W -1 = WT ; that is, WW T = WTW = I .
Definition 1.3
A square matrix A is called orthogonal if AAT = ATA = I.
Note
A is orthogonal if and only if A is non-singular and AŌłÆ1 = AT .
Example 1.11
Prove that 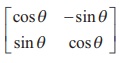 is orthogonal.
is orthogonal.
Solution
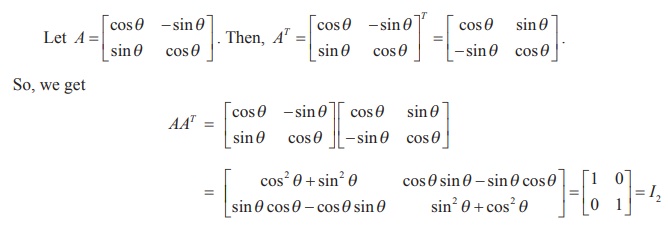
Similarly,
we get ATA = I2 . Hence AAT = ATA =
I2 ŌćÆ
A is orthogonal.
Example 1.12
If A = 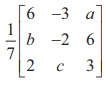 , is orthogonal, find a, b and c ,
and hence AŌłÆ1.
, is orthogonal, find a, b and c ,
and hence AŌłÆ1.
Solution
If A is orthogonal, then AAT = AT A = I3
. So, we have
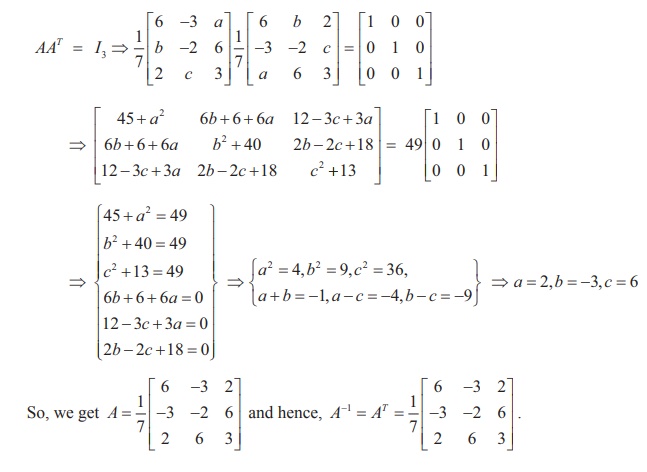
Related Topics