Definition, Theorem, Formulas, Solved Example Problems | Elementary Transformations of a Matrix - Gauss Jordan Method | 12th Mathematics : UNIT 1 : Applications of Matrices and Determinants
Chapter: 12th Mathematics : UNIT 1 : Applications of Matrices and Determinants
Gauss Jordan Method
Gauss-Jordan Method
Let A be a non-singular square matrix of order n .
Let B be the inverse of A.
Then, we have AB = BA = In . By the property of In ,
we have A = In A = AIn .
Consider the equation A = In A …………………………………………..(1)
Since A is non-singular, pre-multiplying by a sequence of
elementary matrices (row operations) on both sides of (1), A on the
left-hand-side of (1) is transformed to the identity matrix In and
the same sequence of elementary matrices (row operations) transforms In
of the right-hand-side of (1) to a matrix B. So, equation (1) transforms
to In = BA. Hence, the inverse of A is B. That is,
A−1 = B.
Note
If E1 , E2 ,L, Ek are
elementary matrices (row operations) such that (Ek L E2 E1
) A = In ,
then A−1 = Ek L E2 E1.
Transforming a non-singular matrix A to the form In
by applying elementary row operations, is called Gauss-Jordan method. The steps in finding A−1 by Gauss-Jordan
method are given below:
Step 1
Augment the identity
matrix In on the right-side of A to get the matrix [ A | In
] .
Step 2
Obtain elementary
matrices (row operations) E1 , E2 ,L, Ek such
that (Ek L E2 E1
) A = In .
Apply E1
, E2 ,L, Ek on
[ A | In
] . Then [(Ek …… E2 E1 ) A | (Ek ….. E2 E1 ) In].
That is, [In | A−1 ].
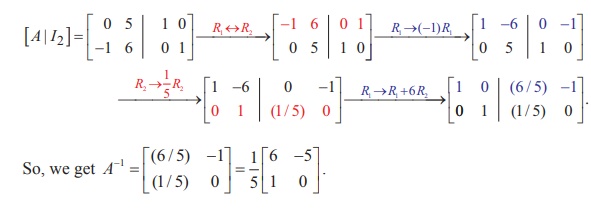
Example 1.20
Find the inverse of the non-singular matrix A = 
, by
Gauss-Jordan method.
Solution
Applying Gauss-Jordan method, we get
Example 1.21
Find the inverse of A =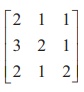 
by Gauss-Jordan method.
Solution
Applying Gauss-Jordan method, we get
Related Topics