Definition, Theorem, Formulas, Solved Example Problems | Elementary Transformations of a Matrix - Rank of a Matrix | 12th Mathematics : UNIT 1 : Applications of Matrices and Determinants
Chapter: 12th Mathematics : UNIT 1 : Applications of Matrices and Determinants
Rank of a Matrix
Rank of a Matrix
To define the rank of a matrix, we have to know about sub-matrices
and minors of a matrix.
Let A be a given matrix. A matrix obtained by deleting some
rows and some columns of A is called a sub-matrix of A. A matrix is a sub-matrix of itself
because it is obtained by leaving zero number of rows and zero number of
columns.
Recall that the determinant of a square sub-matrix of a matrix
is called a minor of the matrix.
Definition 1.6
The rank of a matrix A is defined as the order of a highest order
non-vanishing minor of the matrix A. It is denoted by the symbol Žü (A). The rank of
a zero matrix is defined to be 0.
Note
i.
If a matrix contains at-least one non-zero element, then Žü ( A) Ōēź 1.
ii.
The rank of the identity matrix In is n.
iii.
If the rank of a matrix A is r, then there exists
at-least one minor of A of order r which does not vanish and
every minor of A of order r +1 and higher order (if any) vanishes.
iv.
If A is an m ├Ś n matrix, then Žü (A) Ōēż min{m, n} = minimum of m, n.
v.
A square matrix A of order n has inverse if and
only if Žü ( A) = n.
Example 1.15
Find the rank of each of the following matrices:
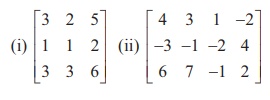
Solution
(i) Let A =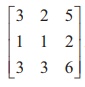 . Then A is a matrix of order 3├Ś 3. So Žü(A) Ōēż
min {3, 3} = 3. The highest order of minors of A is 3 . There is only one
third order minor of A .
. Then A is a matrix of order 3├Ś 3. So Žü(A) Ōēż
min {3, 3} = 3. The highest order of minors of A is 3 . There is only one
third order minor of A .
It is  = 3 (6ŌłÆ 6) ŌłÆ 2 (6ŌłÆ6) + 5 (3 ŌłÆ 3) = 0. So, Žü(A) < 3.
= 3 (6ŌłÆ 6) ŌłÆ 2 (6ŌłÆ6) + 5 (3 ŌłÆ 3) = 0. So, Žü(A) < 3.
Next consider the
second-order minors of A .
We find that the second order minor 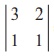 = 3 ŌłÆ 2 = 1 ŌēĀ 0 .
So Žü(A) = 2 .
= 3 ŌłÆ 2 = 1 ŌēĀ 0 .
So Žü(A) = 2 .
(ii) Let A = 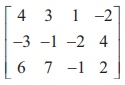 . Then A is a matrix of order 3├Ś4 . So Žü(A)
Ōēż min {3, 4} = 3.
. Then A is a matrix of order 3├Ś4 . So Žü(A)
Ōēż min {3, 4} = 3.
The highest order of minors of A is 3 . We search for a non-zero
third-order minor of A . But
we find that all of them vanish. In fact, we have
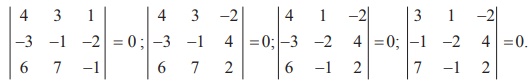
So, Žü(A) < 3. Next, we search for a non-zero second-order minor of A .
We find that 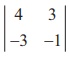 = -4+9 =5 ŌēĀ 0 . So, Žü(A) = 2 .
= -4+9 =5 ŌēĀ 0 . So, Žü(A) = 2 .
Remark
Finding the rank of a matrix by searching a highest order
non-vanishing minor is quite tedious when the order of the matrix is quite
large. There is another easy method for finding the rank of a matrix even if
the order of the matrix is quite high. This method is by computing the rank of
an equivalent row-echelon form of the matrix. If a matrix is in row-echelon
form, then all entries below the leading diagonal (it is the line
joining the positions of the diagonal elements a11 , a22
, a33 ,L. of the matrix) are
zeros. So, checking whether a minor is zero or not, is quite simple.
Example 1.16
Find the rank of the following matrices which are in row-echelon
form :
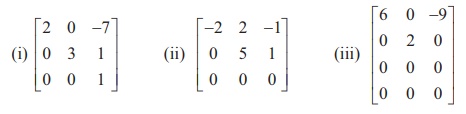
Solution
(i) Let A = 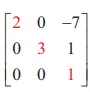 . Then A is a matrix of order 3 3 ├Ś and Žü(A)
Ōēż 3
. Then A is a matrix of order 3 3 ├Ś and Žü(A)
Ōēż 3
The third order minor |A| =  = (2) (3)( 1) = 6 ŌēĀ 0 . So, Žü(A) = 3 .
= (2) (3)( 1) = 6 ŌēĀ 0 . So, Žü(A) = 3 .
Note that there are
three non-zero rows.
(ii) Let A =  . Then A is a matrix of order 3├Ś 3 and Žü(A)
Ōēż 3.
. Then A is a matrix of order 3├Ś 3 and Žü(A)
Ōēż 3.
The only third order minor is |A| =  = (-2) (5) (0) = 0
. So Žü(A) Ōēż 2 .
= (-2) (5) (0) = 0
. So Žü(A) Ōēż 2 .
There are several second order minors. We find that there is a
second order minor, for example, 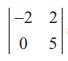 = (-2)(5) = -10 ŌēĀ 0 . So, Žü(A) = 2.
= (-2)(5) = -10 ŌēĀ 0 . So, Žü(A) = 2.
Note that there are
two non-zero rows. The third row is a zero row.
(iii) Let A = 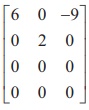 . Then A is a matrix of order 4 ├Ś 3 and
Žü(A) Ōēż 3.
. Then A is a matrix of order 4 ├Ś 3 and
Žü(A) Ōēż 3.
The last two rows are zero rows. There are several second order
minors. We find that there is a second
order minor, for example, 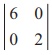 =
(6) (2) = 12 ŌēĀ 0 . So, Žü(A) = 2.
=
(6) (2) = 12 ŌēĀ 0 . So, Žü(A) = 2.
Note that there are
two non-zero rows. The third and fourth rows are zero rows.
We observe from the above example that the rank of a matrix in row
echelon form is equal to the number of
non-zero rows in it. We state this observation as a theorem without proof.
Theorem
1.11
The rank of a matrix in row echelon form is the number of
non-zero rows in it.
The rank of a matrix which is not in a row-echelon form, can be
found by applying the following result which is stated without proof.
Theorem
1.12
The rank of a non-zero matrix is equal to the number of non-zero
rows in a row-echelon form of the matrix.
Example 1.17
Find the rank of the matrix 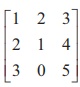 by reducing it to a
row-echelon form.
by reducing it to a
row-echelon form.
Solution
Let A =  . Applying elementary row operations, we get
. Applying elementary row operations, we get

The
last equivalent matrix is in row-echelon form. It has two non-zero rows. So, Žü
(A)= 2.
Example 1.18
Find the rank of the matrix 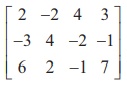 by reducing it to a
row-echelon form.
by reducing it to a
row-echelon form.
Solution
Let
A be the matrix. Performing elementary row operations, we get
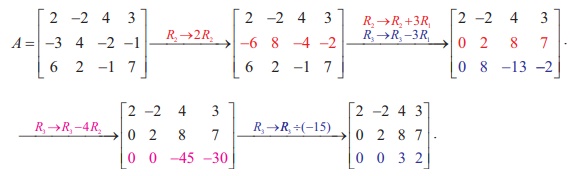
The
last equivalent matrix is in row-echelon form. It has three non-zero rows. So,
Žü(A) = 3 .
Elementary
row operations on a matrix can be performed by pre-multiplying the given matrix
by a special class of matrices called elementary matrices.
Definition 1.7
An elementary matrix is defined as a matrix which is obtained from an
identity matrix by applying only one elementary transformation.
Remark
If we are dealing with matrices with three rows, then all
elementary matrices are square matrices of order 3 which are obtained by
carrying out only one elementary row operations on the unit matrix I3.
Every elementary row operation that is carried out on a given matrix A can
be obtained by pre-multiplying A with elementary matrix. Similarly,
every elementary column operation that is carried out on a given matrix A can
be obtained by post-multiplying Awith an elementary matrix. In the
present chapter, we use elementary row operations only.
For instance, let us consider the matrix A = 
Suppose that we do the transformation R2 ŌåÆ R2 + ╬╗R3 on A, where
╬╗ ŌēĀ 0 is a constant. Then, we get
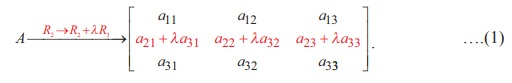
The matrix 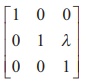 is
an elementary matrix, since we have
is
an elementary matrix, since we have 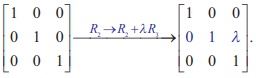
Pre-multiplying A by  , we get
, we get
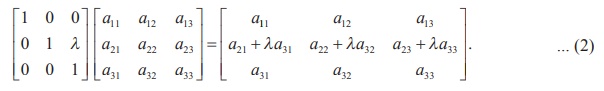
From (1) and (2), we get 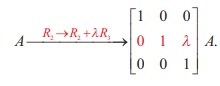
So, the effect of applying the elementary transformation R2
ŌåÆ R2 + ╬╗R3 on A is the same as that of pre-multiplying
the matrix A with the elementary matrix 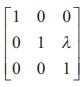
Similarly, we can show that
(i) the effect of applying the elementary transformation R2Ōåö
R3 on A is the same as that of
pre-multiplying the matrix A with the elementary matrix 
(ii) the effect of applying the elementary transformation R2 ŌåÆ
R2╬╗ on A is the same as that of
pre-multiplying the matrix A with the elementary matrix 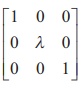
We state the following result without proof.
Theorem 1.13
Every non-singular matrix can be transformed to an identity
matrix, by a sequence of elementary row operations.
As an illustration of the above theorem, let us consider the
matrix A = 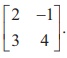
Then, |A| = 12+ 3 = 15 ŌēĀ 0. So, A is non-singular. Let us transform A into I2 by a sequence of elementary row operations. First, we search for a row operation to make a11 of A as 1. The elementary row operation needed for this is R1 ŌåÆ (1/2) R1. The corresponding elementary matrix is
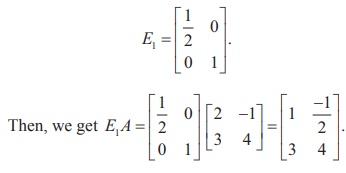
Next, let us make all elements below a11 of E1A
as 0. There is only one element a21.
The elementary row operation needed for this is R2 ŌåÆ R2 + (ŌłÆ3) R1 .
The corresponding elementary matrix is E2 =
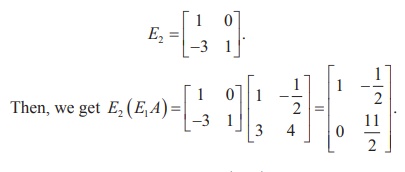
Next, let us make a22 of E2(E2A)
as 1. The elementary row operation needed for this is 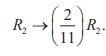
The corresponding elementary matrix is E3 = 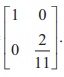
Then, we get E3(E2(E1A)) = 
Finally, let us find an elementary row operation to make a12
of E3(E2(E1A)) as 0. The elementary row operation needed for this is R1
ŌåÆ R1 + (1/2) R2. The corresponding elementary matrix is
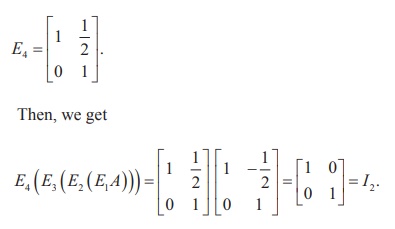
We write the above sequence of elementary transformations in the
following manner:

Example 1.19
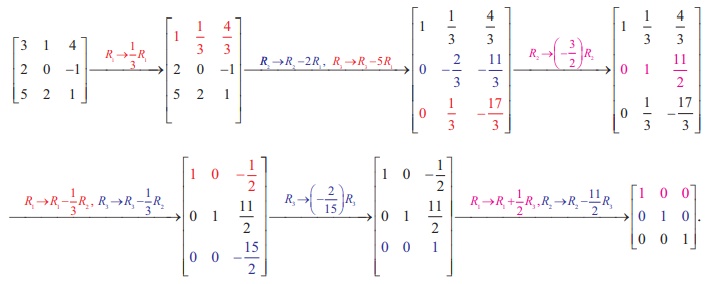
Show that the matrix 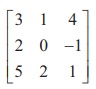 is non-singular and reduce
it to the identity matrix by elementary row transformations.
is non-singular and reduce
it to the identity matrix by elementary row transformations.
Solution
Let A = 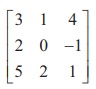 .Then, |A| = 3 (0+2 ) ŌĆō 1(2+5) + 4(4-0) = 6-7+16
ŌēĀ 0. So, A is non-singular. Keeping the identity matrix as our goal, we perform
the row operations sequentially on A as follows:
.Then, |A| = 3 (0+2 ) ŌĆō 1(2+5) + 4(4-0) = 6-7+16
ŌēĀ 0. So, A is non-singular. Keeping the identity matrix as our goal, we perform
the row operations sequentially on A as follows:
Related Topics