Definition, Theorem, Formulas, Solved Example Problems | Elementary Transformations of a Matrix - Row Echelon form | 12th Mathematics : UNIT 1 : Applications of Matrices and Determinants
Chapter: 12th Mathematics : UNIT 1 : Applications of Matrices and Determinants
Row Echelon form
Row-Echelon form
Using the row elementary operations, we can transform a given
non-zero matrix to a simplified form called a Row-echelon form. In a row-echelon
form, we may have rows all of whose entries are zero. Such rows are called zero rows. A non-zero row is
one in which at least one of the entries is not zero. For instance, in the
matrix,
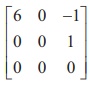 ,
,
R1 and R2 are non-zero rows and R3
is a zero row
Definition 1.5
A non-zero matrix E
is said to be in a row-echelon form if:
i.
All zero rows of E occur below every non-zero row of E.
ii.
The first non-zero element in any row i of E occurs
in the jth column of E , then all other entries in the
jth column of E below the first non-zero element of
row i are zeros.
iii.
The first non-zero entry in the ith row of E lies
to the left of the first non-zero entry in (i +1)th row of E .
Note
A non-zero matrix is in a row-echelon form if all zero rows
occur as bottom rows of the matrix, and if the first non-zero element in any
lower row occurs to the right of the first non- zero entry in the higher row.
The following matrices are in row-echelon form:

Consider the matrix in (i). Go up row by row from the last row of
the matrix. The third row is a zero row. The first non-zero entry in the second
row occurs in the third column and it lies to the right of the first non-zero
entry in the first row which occurs in the second column. So the matrix is in
row- echelon form.
Consider the matrix in (ii). Go up row by row from the last row of
the matrix. All the rows are non-zero rows. The first non-zero entry in the
third row occurs in the fourth column and it occurs to the right of the first
non-zero entry in the second row which occurs in the third column. The first
non-zero entry in the second row occurs in the third column and it occurs to
the right of the first non-zero entry in the first row which occurs in the
first column. So the matrix is in row-echelon form.
The following matrices are not in row-echelon form:

Consider the matrix in (i). In this matrix, the first non-zero
entry in the third row occurs in the second column and it is on the left of the
first non-zero entry in the second row which occurs in the third column. So the
matrix is not in row-echelon form.
Consider the matrix in (ii). In this matrix, the first non-zero
entry in the second row occurs in the first column and it is on the left of the
first non-zero entry in the first row which occurs in the second column. So the
matrix is not in row-echelon form.
Method to reduce a matrix [aij]m √ón to a row-echelon form.
Step 1
Inspect the first row. If the first row is a zero row, then the
row is interchanged with a non-zero row below the first row. If a11
is not equal to 0, then go to step 2. Otherwise, interchange the first row R1
with any other row below the first row which has a non-zero element in the
first column; if no row below the first row has non-zero entry in the first
column, then consider a12 . If a12 is not
equal to 0, then go to step 2. Otherwise, interchange the first row R1
with any other row below the first row which has a non-zero element in the
second column; if no row below the first row has non-zero entry in the second
column, then consider a13. Proceed in the same way till we
get a non-zero entry in the first row. This is called pivoting and the first non-zero
element in the first row is called the pivot of the first row.
Step 2
Use the first row and elementary row operations to transform all
elements under the pivot to become zeros.
Step 3
Consider the next row as first row and perform steps 1 and 2 with
the rows below this row only.
Repeat the step until all rows are exhausted.
Example 1.13
Reduce the matrix  to a row-echelon form.
to a row-echelon form.
Solution

Note
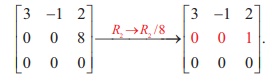
This
is also a row-echelon form of the given matrix.
So,
a row-echelon form of a matrix is not necessarily
unique.
Example 1.14
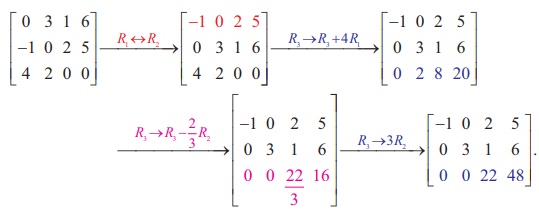
Reduce the matrix 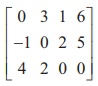 to a row-echelon form.
to a row-echelon form.
Solution
Related Topics