Definition, Theorem, Formulas, Solved Example Problems | Inverse of a Non-Singular Square Matrix - Definition of inverse matrix of a square matrix | 12th Mathematics : UNIT 1 : Applications of Matrices and Determinants
Chapter: 12th Mathematics : UNIT 1 : Applications of Matrices and Determinants
Definition of inverse matrix of a square matrix
Definition of inverse matrix of a square matrix
Now, we define the
inverse of a square matrix.
Definition 1.2
Let A be a
square matrix of order n. If there exists a square matrix B of
order n such that AB = BA = In , then the matrix B is called an inverse
of A.
Theorem 1.2
If a square matrix has an inverse, then it is unique.
Proof
Let A be a square matrix order n such that an
inverse of A exists. If possible, let there be two inverses B and
C of A. Then, by definition, we have AB = BA = In and
AC = CA = In
Using these equations,
we get
C = CIn = C( AB) = (CA)B = InB = B.
Hence the uniqueness
follows.
Notation The inverse of a matrix A is denoted by AŌłÆ1.
Note
AAŌłÆ1 = AŌłÆ1 A = In .
Theorem 1.3
Let A be square matrix of order n. Then, AŌłÆ1 exists if and only if
A is non-singular.
Proof
Suppose that AŌłÆ1 exists. Then AAŌłÆ1 = AŌłÆ1 A = In .
By the product rule for determinants, we get
det( AAŌłÆ1 ) =
det( A) det( AŌłÆ1 ) =
det( AŌłÆ1 ) det( A) =
det(In ) =
1. So, |A| =
det( A) ŌēĀ
0.
Hence A is
non-singular.
Conversely, suppose that A is non-singular.
Then |A | ŌēĀ 0. By Theorem 1.1, we
get
A(adj A) = (adj A) A = |A| In.
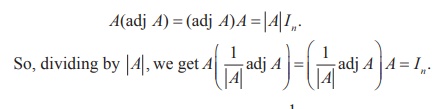
Thus,
we are able to find a matrix B = 1/|A| adj A
such that AB = BA = In .
Hence,
the inverse of A exists and it is
given by 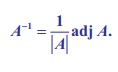
Remark
The determinant of a
singular matrix is 0 and so a singular matrix has no inverse.
Example 1.2
If A = 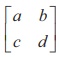 is non-singular, find AŌłÆ1
is non-singular, find AŌłÆ1
Solution
We first find adj A. By
definition, we get
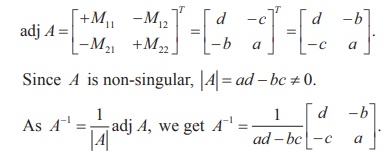
Example 1.3
Find the inverse of the matrix 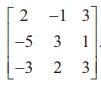
Solution
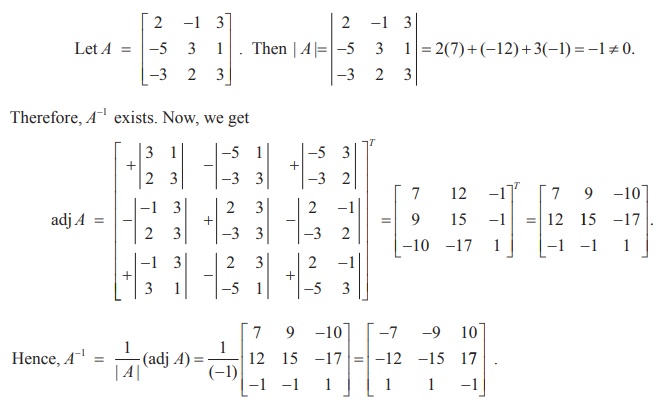
Related Topics