Definition, Theorem, Formulas, Solved Example Problems | Applications of Matrices: Consistency of System of Linear Equations by Rank Method - Matrix: Homogeneous system of linear equations | 12th Mathematics : UNIT 1 : Applications of Matrices and Determinants
Chapter: 12th Mathematics : UNIT 1 : Applications of Matrices and Determinants
Matrix: Homogeneous system of linear equations
Applications of Matrices: Consistency of System of Linear Equations by Rank Method
In second previous section, we have already defined consistency of a system of linear equation. In this section, we investigate it by using rank method. We state the following theorem without proof:
Theorem 1.14 (Rouch├® - Capelli Theorem)
A system of linear equations, written in the matrix form as AX = B, is consistent if and only if the rank of the coefficient matrix is equal to the rank of the augmented matrix; that is, Žü ( A) = Žü ([ A | B]).
We apply the theorem in the following examples.
Homogeneous system of linear equations
We recall that a
homogeneous system of linear equations is given by
a11x1 + a12x2 + a13x3 + ŌĆ”ŌĆ”ŌĆ” + a1nxn + = 0
a21x1 + a22x2 + a23x3 + ŌĆ”ŌĆ”ŌĆ” + a2nxn + = 0
a31x1 + a32x2 + a3x3 + ŌĆ”ŌĆ”ŌĆ” + a3nxn + = 0
ŌĆ”.. ŌĆ”. ŌĆ”..
ŌĆ”.. ŌĆ”.. ...
am1x1 + am2x2 + am3x3 + ŌĆ”ŌĆ”ŌĆ” + amnxn + = 0 ŌĆ”ŌĆ”ŌĆ”(1)
where the
coefficients aij , i = 1, 2,ŌĆ”., m; j = 1,
2,ŌĆ”., n are constants. The above system is always satisfied by x1 = 0, x2 = 0,ŌĆ”.,, xn = 0.This solution is
called the trivial
solution of
(1). In other words, the system (1) always possesses a solution.
The above system (1) can be put in the matrix form AX = Omx1, where

We will denote Om ├Ś 1 simply by the capital letter O. Since O
is the zero column matrix, it is always true that Žü ( A)
= Žü ([ A | O]) Ōēż
m. So,
by Rouch├® - Capelli Theorem, any system of homogeneous linear equations is always consistent.
Suppose that m < n, then there are more number of unknowns than the number
of equations. So Žü ( A) = Žü ([ A | O]) < n. Hence, system (1) possesses a non-trivial solution.
Suppose that m = n, then there are equal number of equations and
unknowns:
a11x1 + a12x2 + a13x3 + ŌĆ”ŌĆ”ŌĆ” + a1nxn + = 0
a21x1 + a22x2 + a23x3 + ŌĆ”ŌĆ”ŌĆ” + a2nxn + = 0
a31x1 + a32x2 + a3x3 + ŌĆ”ŌĆ”ŌĆ” + a3nxn + = 0
ŌĆ”.. ŌĆ”. ŌĆ”..
ŌĆ”.. ŌĆ”.. ...
an1x1 + an2x2 + an3x3 + ŌĆ”ŌĆ”ŌĆ” + annxn + = 0 ŌĆ”ŌĆ”ŌĆ”(1)
Two cases arise.
Case (i)
If Žü ( A) = Žü ([ A | O])
= n, then system (2) has a unique solution and it is the trivial solution.
Since Žü ( A) = n, |A| ŌēĀ 0. So for trivial solution | A | ŌēĀ 0 .
Case (ii)
If Žü ( A) = Žü ([ A | O])
< n, then system (2) has a non-trivial solution. Since Žü ( A) < n, |A|
=0.
In other words, the homogeneous system
(2) has a non-trivial solution if and only if the determinant of the
coefficient matrix is zero.
Suppose that m > n, then there
are more number of equations than the number of unknowns.
Reducing the system by
elementary transformations, we get Žü (A) = Žü ([ A | O]) Ōēż n.
Example 1.35
Solve the following
system:
x + 2y + 3z = 0, 3x +
4y + 4z = 0, 7x + 10y + 12z =0.
Solution
Here the number of
equations is equal to the number of unknowns.
Transforming into
echelon form (Gaussian elimination method), the augmented matrix becomes
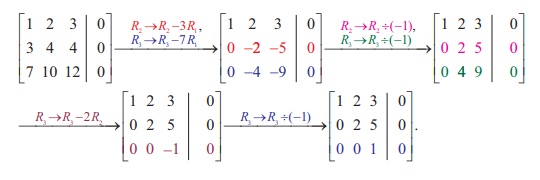
So, Žü(A) = Žü([A| O]) = 3
= Number of unknowns
Hence, the system has a
unique solution. Since x = 0, y = 0, z = 0 is always a solution of the
homogeneous system, the only solution is the trivial solution x = 0, y = 0, z =
0.
Note
In the above example, we
find that
|A|= 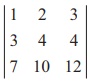 =
1(48-40) - 2(36-28) + 3(30-28) = 8-16+6 = -2 ŌēĀ 0.
=
1(48-40) - 2(36-28) + 3(30-28) = 8-16+6 = -2 ŌēĀ 0.
Example 1.36
Solve the system: x +
3y ŌłÆ 2z = 0, 2x ŌłÆ y + 4z = 0, x ŌłÆ11y +14z = 0.
Solution
Here the number of
unknowns is 3.
Transforming into
echelon form (Gaussian elimination method), the augmented matrix becomes
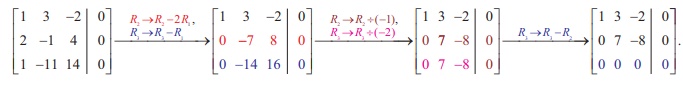
So, Žü(A) = Žü ([A |
O ] ) = 2 < 3 = Number of unknowns
Hence, the system has a
one parameter family of solutions.
Writing the equations
using the echelon form, we get
x + 3y ŌĆō 2z =0, 7y ŌĆō 8z
= 0, 0 = 0.
Taking z = t, where t is
an arbitrary real number, we get by back substitution,
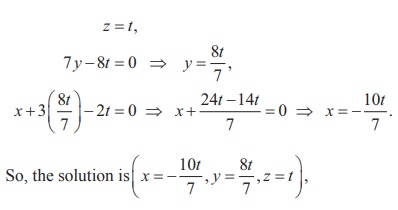
, where is any real
number.
Example 1.37
Solve the system: x + y ŌłÆ 2z = 0, 2x ŌłÆ 3y + z = 0, 3x ŌłÆ 7 y +10z = 0, 6x ŌłÆ 9 y +10z = 0.
Solution
Here the number of
equations is 4 and the number of unknowns is 3. Reducing the augmented matrix
to echelon-form, we get

So, Žü(A) = Žü([A|O]) = 3
= Number of unknowns
Hence the system has
trivial solution only.
Example 1.38
Determine the values of ╬╗ for which the following system of
equations
(3╬╗ ŌĆō 8 )x + 3y + 3z =0, 3x+(3╬╗-8)y + 3z = 0, 3x + 3y +
(3╬╗ -8)z = 0
has a non-trivial solution.
Solution
Here the number of
unknowns is 3. So, if the system is consistent and has a non-trivial solution,
then the rank of the coefficient matrix is equal to the rank of the augmented
matrix and is less than 3. So the determinant of the coefficient matrix
should be 0.
Hence we get
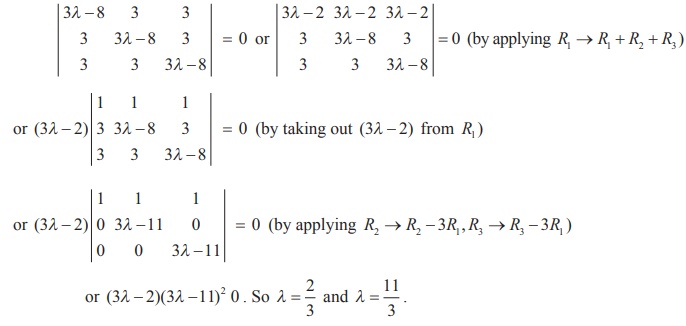
We now give an application of system of linear homogeneous equations to chemistry. You are already aware of balancing chemical reaction equations by inspecting the number of atoms present on both sides. A direct method is explained as given below.
Example 1.39
By using Gaussian elimination method, balance the chemical
reaction equation:
C5H8 + O2 ŌåÆ CO2 + H2O.
(The above is the
reaction that is taking place in the burning of organic compound called
isoprene.)
Solution
We are searching for
positive integers x1, x2, x3 and x4 such that
x1C5H8 + x2O2 = x3CO2 + x4H2O
....
(1)
The number of carbon
atoms on the left-hand side of (1) should be equal to the number of carbon
atoms on the right-hand side of (1). So we get a linear homogenous
equation
5x1 = x3 ŌćÆ 5x1 ŌĆō x3 =0
ŌĆ”ŌĆ”..(2)
Similarly, considering
hydrogen and oxygen atoms, we get respectively,
8x1 = 2x4 ŌćÆ 4x1 ŌĆō x4 = 0, ŌĆ”ŌĆ”. (3)
2x2 = 2x3 + x4 ŌćÆ 2x2 ŌĆō 2x3 ŌĆō x4 =
0. ... (4)
Equations (2), (3), and
(4) constitute a homogeneous system of linear equations in four unknowns.
The augmented matrix is
[ A|B] = 
By Gaussian elimination
method, we get
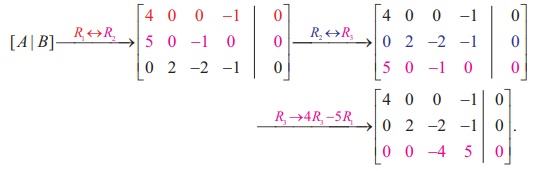
Therefore, Žü(A) =
Žü([A|B]) = 3 < 4 = umber of
unknowns
The system is consistent
and has infinite number of solutions.
Writing the equations
using the echelon form, we get
4x1 ŌĆō x4 = 0, 2x2 - 2x3 - x4 = 0, -4x3 + 5x4 = 0.
So, one of the unknowns
should be chosen arbitrarily as a non-zero real number.
Let us choose x4 = t. t ŌēĀ 0. Then, by
back substitution, we get 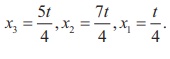
Since x1, x2, x3, and x4 are positive integers,
let us choose t = 4.
Then, we get x1 =1, x2 =7, x3 =5, and x4 = 4.
So, the balanced equation is C5H8 + 7O2 ŌåÆ 5CO2 + H2O.
Example 1.40
If the system of equations px + by + cz = 0, ax + qy + cz =0, ax + by + rz = 0 has a non-trivial solution and p ŌēĀ a, q ŌēĀ b, r ŌēĀ c, prove that
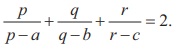
Solution
Assume that the system
px + by + cz = 0, ax + qy + cz = 0, ax + by + rz = 0 has a non-trivial solution
So, we have  =
0.
=
0.
Applying R2 ŌåÆ R2 ŌłÆ R1 and R3 ŌåÆ R3 ŌłÆ R1 and in the above
equation,
we get
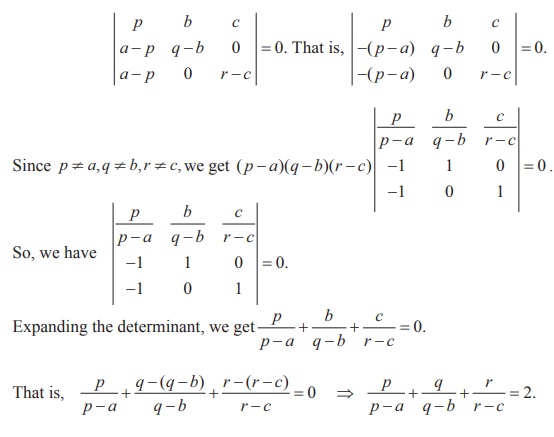
Related Topics