Application of matrices to Cryptography

Application of matrices to Cryptography

One of the important applications of inverse of a non-singular square matrix is in cryptography. Cryptography is an art of communication between two people by keeping the information not known to others. It is based upon two factors, namely encryption and decryption. Encryption means the process of transformation of an information (plain form) into an unreadable form (coded form). On the other hand, Decryption means the transformation of the coded message back into original form. Encryption and decryption require a secret technique which is known only to the sender and the receiver.

This secret is called a key. One way of generating a key is by using a non-singular matrix to encrypt a message by the sender. The receiver decodes (decrypts) the message to retrieve the original message by using the inverse of the matrix. The matrix used for encryption is called encryption matrix (encoding matrix) and that used for decoding is called decryption matrix (decoding matrix).

We explain the process of encryption and decryption by means of an example.

Suppose that the sender and receiver consider messages in alphabets A − Z  only, both assign the numbers 1-26 to the letters A − Z respectively, and the number 0 to a blank space. For simplicity, the sender employs a key as post-multiplication by a non-singular matrix of order 3 of his own choice. The receiver uses post-multiplication by the inverse of the matrix which has been chosen by the sender.

Let the encoding matrix be

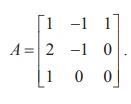
Let the message to be sent by the sender be “WELCOME”.

Since the key is taken as the operation of post-multiplication by a square matrix of order 3, the message is cut into pieces (WEL), (COM), (E), each of length 3, and converted into a sequence of row matrices of numbers:

[23 5 12],[3 15 13],[5 0 0].

Note that, we have included two zeros in the last row matrix. The reason is to get a row matrix with 5 as the first entry.

Next, we encode the message by post-multiplying each row matrix as given below:

So the encoded message is [45 − 28 −23] [46 -18 3] [ 5  −5 5]

The receiver will decode the message by the reverse key, post-multiplying by the inverse of A.

So the decoding matrix is

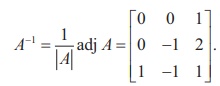
The receiver decodes the coded message as follows:

So, the sequence of decoded row matrices is [23 5 12] ,  [3 15 13], [5 0 0].

Thus, the receiver reads the message as “WELCOME”.