Elementary Transformations of a Matrix

Elementary Transformations of a Matrix

A matrix can be transformed to another matrix by certain operations called elementary row operations and elementary column operations.

Elementary row and column operations

Elementary row (column) operations on a matrix are as follows:

(i) The interchanging of any two rows (columns) of the matrix

(ii) Replacing a row (column) of the matrix by a non-zero scalar multiple of the row (column) by a non-zero scalar.

(iii) Replacing a row (column) of the matrix by a sum of the row (column) with a non-zero scalar multiple of another row (column) of the matrix.

Elementary row operations and elementary column operations on a matrix are known as elementary transformations.

We use the following notations for elementary row transformations:

i.   Interchanging of i^th and j^th rows is denoted by R_i ↔ R_j .

ii. The multiplication of each element of i^th row by a non-zero constant λ is denoted by R_i  â†’ λ R_i .

iii. Addition to i^th row, a non-zero constant λ multiple of j^th row is denoted by R_i → R_i + λ R_j . Similar notations are used for elementary column transformations.

Definition 1.4

Two matrices A and B of same order are said to be equivalent to one another if one can be obtained from the other by the applications of elementary transformations. Symbolically, we write A ~ B to mean that the matrix A is equivalent to the matrix B .

For instance, let us consider a matrix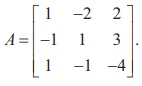 

After performing the elementary row operation R₂ → R₂ + R₁ on A , we get a matrix B in which the second row is the sum of the second row in A and the first row in A .

Thus, we get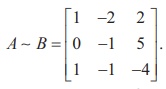 

The above elementary row transformation is also represented as follows:

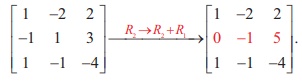
Note

An elementary transformation transforms a given matrix into another matrix which need not be equal to the given matrix.