Summary

SUMMARY

(1) Adjoint of a square matrix A = Transpose of the cofactor matrix of A .

(2) A(adj A) = (adj A) A = A I_n.

(3) A^-1 = [ 1/|A| ] adj A.

(4) , 

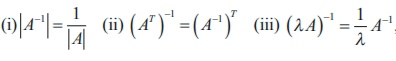where λ is a non-zero scalar.

(5) (i) (AB)^-1 = B^-1 A^-1 . (ii) ((A)^-1 )^-1=A

(6) If A is a non-singular square matrix of order n , then

(8) (i) A matrix A is orthogonal if AA^T = A^T A = I

(ii) A matrix A is orthogonal if and only if A is non-singular and A⁻¹ = A^T

(8) Methods to solve the system of linear equations AX = B

(i) By matrix inversion method X = A^-1B, | A | ≠ 0

(ii) (ii) By Cramer’s rule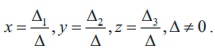 

(iii) By Gaussian elimination method

(9) (i) If ρ ( A) = ρ ([ A | B]) = number of unknowns, then the system has unique solution.

(ii) If ρ ( A) = ρ ([ A | B]) <  number of unknowns, then the system has infinitely many solutions.

(iii) If ρ ( A) ≠ ρ ([ A | B]) then the system is inconsistent and has no solution.

(10) The homogenous system of linear equations AX = 0

(i) has the trivial solution, if | A | ≠ 0 .

(ii) has a non trivial solution, if | A |= 0 .