Solution to a System of Linear equations

Solution to a System of Linear equations

The meaning of solution to a system of linear equations can be understood by considering the following cases :

Case (i)

Consider the system of linear equations

2x - y = 5 ,  ... (1)

x + 3y = 6 . ... (2)

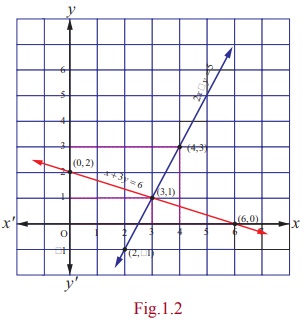
These two equations represent a pair of straight lines in two dimensional analytical geometry (see the Fig. 1.2). Using (1), we get

x  =  [5 + y] / 2     (3)

Substituting (3) in (2) and simplifying, we get y = 1.

 Substituting         y = 1 in (1) and simplifying, we get  x = 3 .

Both equations (1) and (2) are satisfied by x = 3 and y = 1.

That is, a solution of (1) is also a solution of (2).

So, we say that the system is consistent and has unique solution (3,1) . The point (3,1) is the point of intersection of the two lines 2x - y = 5 and x + 3y = 6 .

Case (ii)

Consider the system of linear equations

3x + 2 y = 5 , ... (1)

6x + 4 y = 10 ... (2)

 Using equation (1), we get

x = [5 - 2 y] / 3 ... (3)

Substituting (3) in (2) and simplifying, we get 0 = 0.

This informs us that equation (2) is an elementary transformation of equation (1). In fact, by dividing equation (2) by 2, we get equation (1). It is not possible to find uniquely x and y with just a single equation (1).

So we are forced to assume the value of one unknown, say y = t , where t is any real number.

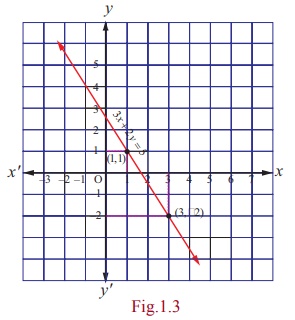
Then, x = [5 - 2t] /3. The two equations (1) and (2) represent one and only one straight line (coincident lines) in two dimensional analytical geometry (see Fig. 1.3) . In other words, the system is consistent (a solution of (1) is also a solution of (2)) and has infinitely many solutions, as t can assume any real value.

Case (iii)

Consider the system of linear equations

4x + y = 6 , ... (1)

8x + 2 y = 18 . ... (2)

Using equation (1), we get

x = [6 – y] / 4 ... (3)

Substituting (3) in (2) and simplifying, we get 12 = 18 .

This is a contradicting result, which informs us that equation (2) is inconsistent with equation (1). So, a solution of (1) is not a solution of (2).

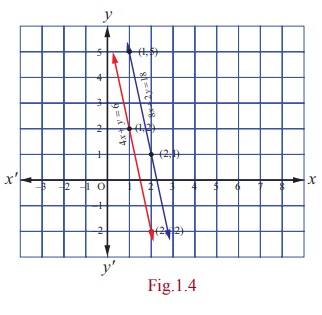
In other words, the system is inconsistent and has no solution. We note that the two equations represent two parallel straight lines (non-coincident) in two dimensional analytical geometry (see Fig. 1.4). We know that two non-coincident parallel lines never meet in real points.

Note

(1) Interchanging any two equations of a system of linear equations does not alter the solution of the system.

(2) Replacing an equation of a system of linear equations by a non-zero constant multiple of itself does not alter the solution of the system.

(3) Replacing an equation of a system of linear equations by addition of itself with a non-zero multiple of any other equation of the system does not alter the solution of the system.

Definition 1.8

A system of linear equations having at least one solution is said to be consistent. A system of linear equations having no solution is said to be inconsistent.

Remark

If the number of the equations of a system of linear equations is equal to the number of unknowns of the system, then the coefficient matrix  A of the system is a square matrix. Further, if  A is a non-singular matrix, then the solution of system of equations can be found by any one of the following methods : (i) matrix inversion method, (ii) Cramer’s rule, (iii) Gaussian elimination method.