Definition, Theorem, Formulas, Solved Example Problems | Inverse of a Non-Singular Square Matrix - Adjoint of a Square Matrix | 12th Mathematics : UNIT 1 : Applications of Matrices and Determinants
Chapter: 12th Mathematics : UNIT 1 : Applications of Matrices and Determinants
Adjoint of a Square Matrix
Adjoint of a Square Matrix
We recall the properties of the cofactors of the elements of a
square matrix. Let A be a square matrix of by order n whose
determinant is denoted | A | or det (
A). Let aij be
the element sitting at the intersection of the ith row and jth
column of A. Deleting the ith row and jth
column of A, we obtain a sub-matrix of order (n ŌłÆ1). The determinant of
this sub-matrix is called minor of the element aij . It is denoted by Mij
.The product of Mij and (ŌłÆ1)i+ j is called cofactor of the element aij
. It is denoted by Aij. Thus the cofactor of aij is Aij = (ŌłÆ1)i+j Mij.
An important property connecting the elements of a square matrix
and their cofactors is that the sum of the products of the entries (elements)
of a row and the corresponding cofactors of the elements of the same row is
equal to the determinant of the matrix; and the sum of the products of the
entries (elements) of a row and the corresponding cofactors of the elements of
any other row is equal to 0. That is,
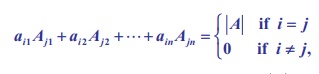
where |A| denotes the determinant of the square matrix A. Here |A| is read as ŌĆ£determinant of A ŌĆØ and not as ŌĆ£ modulus of A ŌĆØ. Note that | A| is just a real number and it can also be negative. For instance, we have
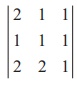 = 2(1ŌłÆ 2) ŌłÆ1(1ŌłÆ 2) +1(2 ŌłÆ 2) = ŌłÆ2 +1+ 0 = ŌłÆ1.
= 2(1ŌłÆ 2) ŌłÆ1(1ŌłÆ 2) +1(2 ŌłÆ 2) = ŌłÆ2 +1+ 0 = ŌłÆ1.
Definition 1.1
Let A be a
square matrix of order n. Then the matrix of cofactors of A is defined
as the matrix obtained by replacing each element aij of A with
the corresponding cofactor Aij. The adjoint matrix of A is defined
as the transpose of the matrix of cofactors of A. It is denoted by adj A.
Note
adj A is a square matrix of order n and adj A = [ Aij ]T = [(ŌłÆ1)i + j Mij ]T
In particular, adj A
of a square matrix of order 3 is given below:
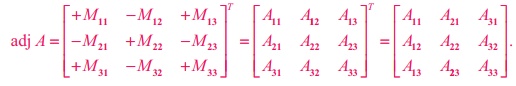
Theorem 1.1
For every square
matrix A of order n , A(adj A) = (adj A) A = |A| In .
Proof
For simplicity, we prove the theorem for n = 3 only.
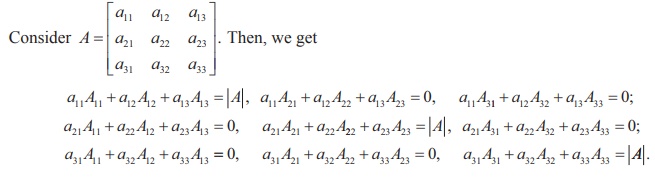
By using the above equations, we get
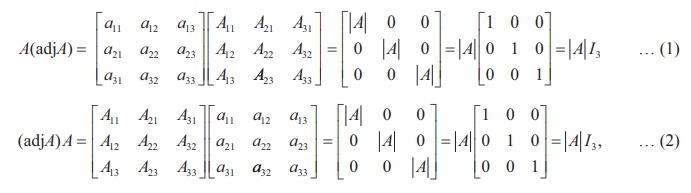
where I3 is the identity matrix of order 3.
So, by equations (1) and (2), we get
A(adj A) = (adj A) A = |A| I3.
Note
If A is a singular matrix of order n , then | A | = 0 and so A(adj
A) = (adj A) A = On ,
where On denotes zero matrix of order n.
Example 1.1
If A = 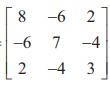 , verify that A (adj A) = (adj A) A = | A | I3 .
, verify that A (adj A) = (adj A) A = | A | I3 .
Solution

Related Topics