Definition, Theorem, Formulas, Solved Example Problems | Applications of Matrices: Consistency of System of Linear Equations by Rank Method - Matrix: Non-homogeneous Linear Equations | 12th Mathematics : UNIT 1 : Applications of Matrices and Determinants
Chapter: 12th Mathematics : UNIT 1 : Applications of Matrices and Determinants
Matrix: Non-homogeneous Linear Equations
Applications of Matrices: Consistency of System of Linear Equations by Rank Method
In second previous section, we have already defined consistency of a system of linear equation. In this section, we investigate it by using rank method. We state the following theorem without proof:
Theorem 1.14 (Rouch├® - Capelli Theorem)
A system of linear equations, written in the matrix form as AX = B, is consistent if and only if the rank of the coefficient matrix is equal to the rank of the augmented matrix; that is, Žü ( A) = Žü ([ A | B]).
We apply the theorem in the following examples.
Non-homogeneous Linear Equations
Example 1.29
Test for consistency of the following system of linear equations and if possible solve:
x + 2 y ŌłÆ z = 3, 3x ŌłÆ y + 2z = 1, x ŌłÆ 2 y + 3z = 3, x ŌłÆ y + z +1 = 0 .
Solution
Here the number of unknowns is 3.
The matrix form of the system is AX = B, where
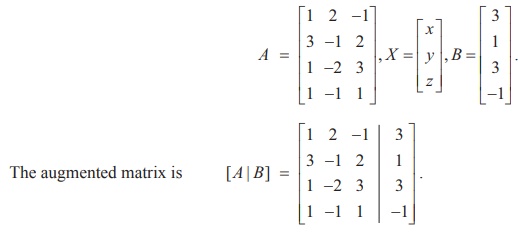
Applying Gaussian elimination method on [ A | B], we get

There are three non-zero rows in the row-echelon form of [A | B].So, Žü ([A | B] ) . = 3
So, the row-echelon form of A is 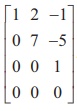 . There are three non-zero rows in it. So Žü(A) = 3.
. There are three non-zero rows in it. So Žü(A) = 3.
Hence, Žü(A) = Žü([ A | B ]) = 3.
From the echelon form, we write the equivalent system of equations
x + 2y ŌĆōz =3, 7y-5z = 8, z=4, 0=0.
The last equation 0 = 0 is meaningful. By the method of back substitution, we get
z = 4
7y - 20 = 8 ŌćÆ y = 4 ,
x = 3 - 8 + 4 ŌćÆ x = ŌłÆ1.
So, the solution is (x = ŌłÆ1, y = 4, z = 4) .(Note that A is not a square matrix.)
Here the given system is consistent and the solution is unique.
Example 1.30
Test for consistency of the following system of linear equations and if possible solve:
4x ŌłÆ 2 y + 6z = 8, x + y ŌłÆ 3z = ŌłÆ1, 15x ŌłÆ 3y + 9z = 21.
Solution
Here the number of unknowns is 3.
The matrix form of the system is AX = B, where
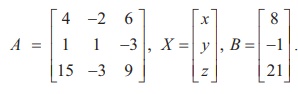
Applying elementary row operations on the augmented matrix[ A | B], we get

So, Žü ( A) = Žü ([ A | B]) = 2 < 3. From the echelon form, we get the equivalent equations
x + y - 3z = -1, y - 3z = -2 , 0 = 0 .
The equivalent system has two non-trivial equations and three unknowns. So, one of the unknowns should be fixed at our choice in order to get two equations for the other two unknowns. We fix z arbitrarily as a real number t , and we get y = 3t - 2, x = -1- (3t - 2) + 3t = 1. So, the solution is ( x =1, y = 3t - 2, z = t ), where t is real . The above solution set is a one-parameter family of solutions.
Here, the given system is consistent and has infinitely many solutions which form a one parameter family of solutions.
Note
In the above example, the square matrix A is singular and so matrix inversion method cannot be applied to solve the system of equations. However,Gaussian elimination method is applicable and we are able to decide whether the system is consistent or not. The next example also confirms the supremacy of Gaussian elimination method over other methods.
Example 1.31
Test for consistency of the following system of linear equations and if possible solve:
x ŌłÆ y + z = ŌłÆ9, 2x ŌłÆ 2 y + 2z = ŌłÆ18, 3x ŌłÆ 3y + 3z + 27 = 0.
Solution
Here the number of unknowns is 3.
The matrix form of the system is AX = B, where
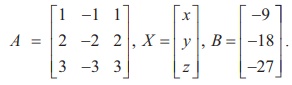
Applying elementary row operations on the augmented matrix[ A | B], we get
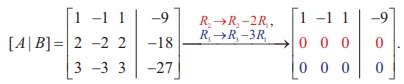
So, Žü ( A) = Žü ([ A | B]) = 1 < 3.
From the echelon form, we get the equivalent equations x - y + z = -9, 0 = 0, 0 = 0.
The equivalent system has one non-trivial equation and three unknowns.
Taking y = s, z = t arbitrarily, we get x - s + t = -9; or x = -9 + s - t.
So, the solution is ( x = -9 + s - t, y = s, z = t ), where s and t are parameters.
The above solution set is a two-parameter family of solutions.
Here, the given system of equations is consistent and has infinitely many solutions which form a two parameter family of solutions.
Example 1.32
Test the consistency of the following system of linear equations
x ŌłÆ y + z = ŌłÆ9, 2x ŌłÆ y + z = 4, 3x ŌłÆ y + z = 6, 4x ŌłÆ y + 2z = 7.
Solution
Here the number of unknowns is 3.
The matrix form of the system of equations is AX = B, where
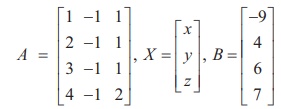
Applying elementary row operations on the augmented matrix [A|B], we get

So, Žü (A) = 3 and Žü ([ A | B]) = 4. Hence Žü ( A) ŌēĀ Žü ([ A | B]).
If we write the equivalent system of equations using the echelon form, we get
x - y + z = -9, y - z = 22, z = -23, 0 = -11.
The last equation is a contradiction.
So the given system of equations is inconsistent and has no solution. By Rouch├® - Capelli theorem, we have the following rule:
┬Ę If there are n unknowns in the system of equations and Žü ( A) = Žü ([ A | B]) = n, then the system AX = B, is consistent and has a unique solution.
┬Ę If there are n unknowns in the system AX = B, and Žü ( A) = Žü ([ A | B]) = n - k, k ŌēĀ 0 then the system is consistent and has infinitely many solutions and these solutions form a k - parameter family. In particular, if there are 3 unknowns in a system of equations and Žü ( A) = Žü ([A | B]) = 2, then the system has infinitely many solutions and these solutions form a one parameter family. In the same manner, if there are 3unknowns in a system of equations and Žü ( A) = Žü ([ A | B]) = 1, then the system has infinitely many solutions and these solutions form a two parameter family.
┬Ę If Žü ( A) ŌēĀ Žü ([ A | B]), then the system AX = B is inconsistent and has no solution.
Example 1.33
Find the condition on a, b and c so that the following system of linear equations has one parameter family of solutions: x + y + z = a, x + 2 y + 3z = b, 3x + 5 y + 7z = c.
Solution
Here the number of unknowns is 3.
The matrix form of the system is AX = B, where A = 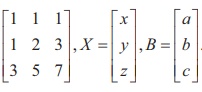
Applying elementary row operations on the augmented matrix [ A | B], we get
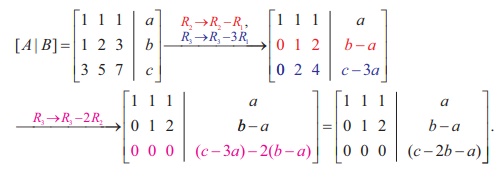
In order that the system should have one parameter family of solutions, we must have Žü ( A) = Žü ([ A, B]) = 2. So, the third row in the echelon form should be a zero row.
So, c - 2b - a = 0 ŌćÆ c = a + 2b.
Example 1.34
Investigate for what values of ╬╗ and ╬╝ the system of linear equations
x + 2 y + z = 7, x + y + ╬╗ z = ╬╝, x + 3y ŌłÆ 5z = 5 has
(i) no solution (ii) a unique solution (iii) an infinite number of solutions.
Solution
Here the number of unknowns is 3.
The matrix form of the system is AX = B, where A = 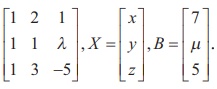
Applying elementary row operations on the augmented matrix [ A | B], we get
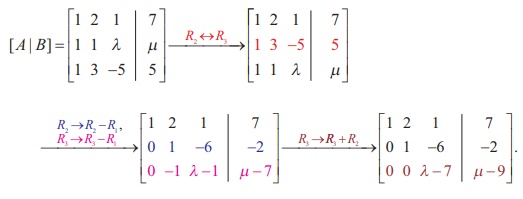
(i) If ╬╗ = 7 and ╬╝ ŌēĀ 9 , then Žü (A) = 2 and Žü ([ A | B]) = 3. So Žü ( A) ŌēĀ Žü ([ A | B]). Hence the given system is inconsistent and has no solution.
(ii) If ╬╗ ŌēĀ 7 and m is any real number, then Žü (A) = 3 and Žü ([ A | B]) = 3.
So Žü (A) = Žü ([ A | B]) = 3 = Number of unknowns. Hence the given system is consistent and has a unique solution.
(iii) If ╬╗ = 7 and ╬╝ = 9, then Žü(A) = 2 and Žü ([ A | B]) = 2.
So, Žü(A) = Žü ([ A | B]) = 2 < Number of unknowns. Hence the given system is consistent and has infinite number of solutions.
Related Topics