Definition, Formulas, Solved Example Problems - Solved Example Problems on Applications of Matrices: Solving System of Linear Equations | 12th Mathematics : UNIT 1 : Applications of Matrices and Determinants
Chapter: 12th Mathematics : UNIT 1 : Applications of Matrices and Determinants
Solved Example Problems on Applications of Matrices: Solving System of Linear Equations
Solution to a System of Linear equations
(i) Matrix Inversion Method
Example 1.22
Solve the following system of linear equations, using matrix inversion method:
5x + 2 y = 3, 3x + 2 y = 5 .
Solution
The matrix form of the system is AX = B , where 
We find |A| = 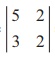 = 10 - 6= 4 ŌēĀ 0. So, AŌłÆ1 exists and AŌłÆ1 =
= 10 - 6= 4 ŌēĀ 0. So, AŌłÆ1 exists and AŌłÆ1 = 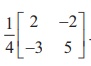
Then, applying the formula X = AŌłÆ1B , we get
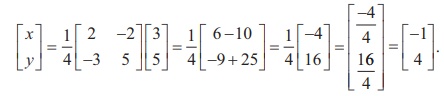
So the solution is (x = ŌłÆ1, y = 4).
Example 1.23
Solve the following system of equations, using matrix inversion method:
2x1 + 3x2 + 3x3 = 5,
x1 ŌĆō 2x2 + x3 = -4,
3x1 ŌĆō x2 ŌĆō 2x3 = 3
Solution
The matrix form of the system is AX = B,where
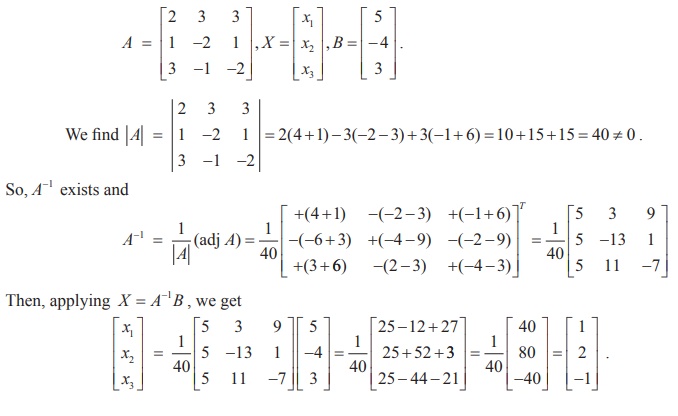
So, the solution is ( x1 = 1, x2 = 2, x3 = ŌłÆ1) .
Example 1.24
If 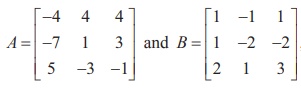 , find the products AB and BA and hence solve the system of equations x ŌłÆ y + z = 4, x ŌĆō 2y ŌĆō 2z = 9, 2x + y +3z =1.
, find the products AB and BA and hence solve the system of equations x ŌłÆ y + z = 4, x ŌĆō 2y ŌĆō 2z = 9, 2x + y +3z =1.
Solution
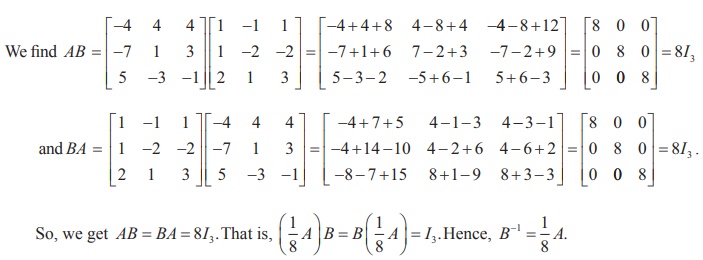
Writing the given system of equations in matrix form, we get
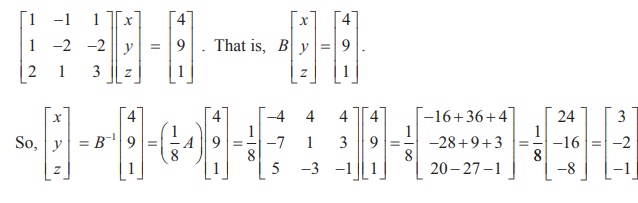
Hence, the solution is (x = 3, y = - 2, z = ŌłÆ1).
(ii) CramerŌĆÖs Rule
Example 1.25
Solve, by CramerŌĆÖs rule, the system of equations
x1 ŌłÆ x2 = 3, 2x1 + 3x2 + 4x3 = 17, x2 + 2x3 = 7.
Solution
First we evaluate the determinants
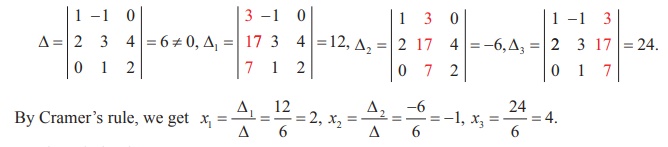
So, the solution is (x1 = 2, x2 = - 1, x3 = 4).
Example 1.26
In a T20 match, Chennai Super Kings needed just 6 runs to win with 1 ball left to go in the last over. The last ball was bowled and the batsman at the crease hit it high up. The ball traversed along a path in a vertical plane and the equation of the path is y = ax2 + bx + c with respect to a xy -coordinate system in the vertical plane and the ball traversed through the points (10,8), (20,16), (30,18) , can you conclude that Chennai Super Kings won the match?

Justify your answer. (All distances are measured in metres and the meeting point of the plane of the path with the farthest boundary line is (70, 0).)
Solution
The path y = ax2 + bx + c passes through the points (10,8), (20,16), (40, 22) . So, we get the system of equations 100a + 10b + c = 8, 400a + 20b + c= 16,1600a + 40b + c = 22. To apply CramerŌĆÖs rule, we find

When x = 70, we get y = 6.
So, the ball went by 6 metres high over the boundary line and it is impossible for a fielder standing even just before theboundary line to jump and catch the ball.
Hence the ball went for a super six and the Chennai Super Kings won the match.
(iii) Gaussian Elimination Method
Example 1.27
Solve the following system of linear equations, by Gaussian elimination method :
4x + 3y + 6z = 25, x + 5 y + 7z = 13, 2x + 9 y + z = 1.
Solution
Transforming the augmented matrix to echelon form, we get

The equivalent system is written by using the echelon form:
x + 5y + 7z = 13 , ŌĆ” (1)
17y + 22z = 27 , ŌĆ” (2)
199z = 398 . ŌĆ” (3)
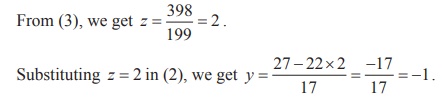
Substituting z = 2, y = -1 in (1), we get x = 13 - 5 ├Ś (ŌłÆ1 ) ŌłÆ 7 ├Ś 2 = 4 .
So, the solution is ( x =4, y = - 1, z = 2 ).
Note. The above method of going from the last equation to the first equation is called the method of back substitution.
Example 1.28
The upward speed v(t) of a rocket at time t is approximated by v(t) = at2 + bt + c, 0 Ōēż t Ōēż 100 where a, b, and c are constants. It has been found that the speed at times t = 3, t = 6 , and t = 9 seconds are respectively, 64, 133, and 208 miles per second respectively. Find the speed at time t = 15 seconds. (Use Gaussian elimination method.)

Solution
Since v(3) =64, v(6) = 133 and v(9) = 208 , we get the following system of linear equations
9a +3b + c = 64 ,
36a + 6b + c = 133,
81a + 9b + c = 208 .
We solve the above system of linear equations by Gaussian elimination method.
Reducing the augmented matrix to an equivalent row-echelon form by using elementary row operations, we get

Writing the equivalent equations from the row-echelon matrix, we get
9a + 3b + c = 64, 2b + c = 41, c= 1.
By back substitution, we get
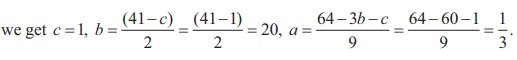
So, we get v (t) = 1/3 t2 + 20t + 1.
Hence, v(15) = 1/3 (225) + 20(15) + 1 = 75 + 300 + 1 = 376
Related Topics