with Answers, Solution - Elementary Transformations of a Matrix: Solved Example Problems | 12th Mathematics : UNIT 1 : Applications of Matrices and Determinants
Chapter: 12th Mathematics : UNIT 1 : Applications of Matrices and Determinants
Elementary Transformations of a Matrix: Solved Example Problems
Row-Echelon form
Example 1.13
Reduce the matrix  to a row-echelon form.
to a row-echelon form.
Solution

Note
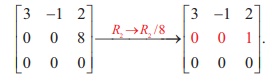
This is also a row-echelon form of the given matrix.
So, a row-echelon form of a matrix is not necessarily unique.
Example 1.14
Reduce the matrix 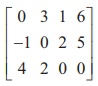 to a row-echelon form.
to a row-echelon form.
Solution
Rank of a Matrix
Example 1.15
Find the rank of each of the following matrices:
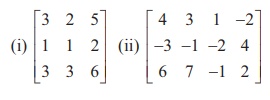
Solution
(i) Let A =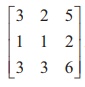 . Then A is a matrix of order 3├Ś 3. So Žü(A) Ōēż min {3, 3} = 3. The highest order of minors of A is 3 . There is only one third order minor of A .
. Then A is a matrix of order 3├Ś 3. So Žü(A) Ōēż min {3, 3} = 3. The highest order of minors of A is 3 . There is only one third order minor of A .
It is  = 3 (6ŌłÆ 6) ŌłÆ 2 (6ŌłÆ6) + 5 (3 ŌłÆ 3) = 0. So, Žü(A) < 3.
= 3 (6ŌłÆ 6) ŌłÆ 2 (6ŌłÆ6) + 5 (3 ŌłÆ 3) = 0. So, Žü(A) < 3.
Next consider the second-order minors of A .
We find that the second order minor 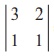 = 3 ŌłÆ 2 = 1 ŌēĀ 0 . So Žü(A) = 2 .
= 3 ŌłÆ 2 = 1 ŌēĀ 0 . So Žü(A) = 2 .
(ii) Let A = 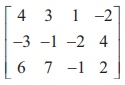 . Then A is a matrix of order 3├Ś4 . So Žü(A) Ōēż min {3, 4} = 3.
. Then A is a matrix of order 3├Ś4 . So Žü(A) Ōēż min {3, 4} = 3.
The highest order of minors of A is 3 . We search for a non-zero third-order minor of A . But
we find that all of them vanish. In fact, we have
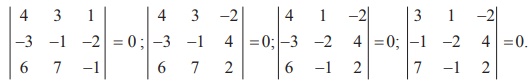
So, Žü(A) < 3. Next, we search for a non-zero second-order minor of A .
We find that 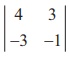 = -4+9 =5 ŌēĀ 0 . So, Žü(A) = 2 .
= -4+9 =5 ŌēĀ 0 . So, Žü(A) = 2 .
Remark
Finding the rank of a matrix by searching a highest order non-vanishing minor is quite tedious when the order of the matrix is quite large. There is another easy method for finding the rank of a matrix even if the order of the matrix is quite high. This method is by computing the rank of an equivalent row-echelon form of the matrix. If a matrix is in row-echelon form, then all entries below the leading diagonal (it is the line joining the positions of the diagonal elements a11 , a22 , a33 ,L. of the matrix) are zeros. So, checking whether a minor is zero or not, is quite simple.
Example 1.16
Find the rank of the following matrices which are in row-echelon form :
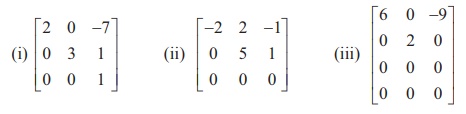
Solution
(i) Let A = 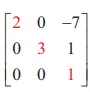 . Then A is a matrix of order 3 3 ├Ś and Žü(A) Ōēż 3
. Then A is a matrix of order 3 3 ├Ś and Žü(A) Ōēż 3
The third order minor |A| =  = (2) (3)( 1) = 6 ŌēĀ 0 . So, Žü(A) = 3 .
= (2) (3)( 1) = 6 ŌēĀ 0 . So, Žü(A) = 3 .
Example 1.17
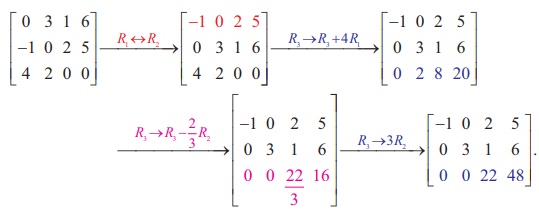
Find the rank of the matrix 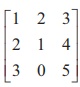 by reducing it to a row-echelon form.
by reducing it to a row-echelon form.
Solution
Let A =  . Applying elementary row operations, we get
. Applying elementary row operations, we get

The last equivalent matrix is in row-echelon form. It has two non-zero rows. So, Žü (A)= 2.
Example 1.18
Find the rank of the matrix 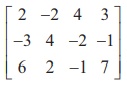 by reducing it to a row-echelon form.
by reducing it to a row-echelon form.
Solution
Let A be the matrix. Performing elementary row operations, we get
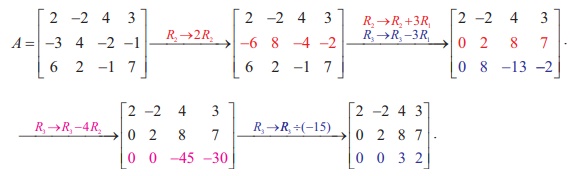
The last equivalent matrix is in row-echelon form. It has three non-zero rows. So, Žü(A) = 3 .
Elementary row operations on a matrix can be performed by pre-multiplying the given matrix by a special class of matrices called elementary matrices.
Example 1.19
Show that the matrix 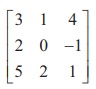 is non-singular and reduce it to the identity matrix by elementary row transformations.
is non-singular and reduce it to the identity matrix by elementary row transformations.
Solution
Let A = 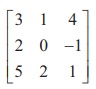 .Then, |A| = 3 (0+2 ) ŌĆō 1(2+5) + 4(4-0) = 6-7+16 ŌēĀ 0. So, A is non-singular. Keeping the identity matrix as our goal, we perform the row operations sequentially on A as follows:
.Then, |A| = 3 (0+2 ) ŌĆō 1(2+5) + 4(4-0) = 6-7+16 ŌēĀ 0. So, A is non-singular. Keeping the identity matrix as our goal, we perform the row operations sequentially on A as follows:
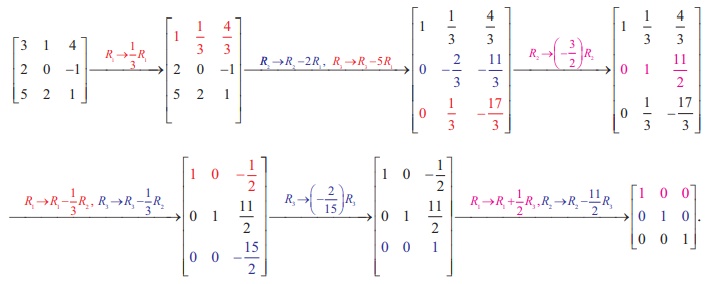
Gauss-Jordan Method
Example 1.20
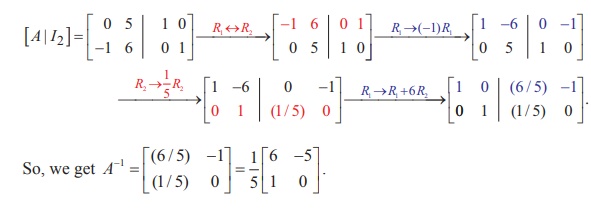
Find the inverse of the non-singular matrix A =  , by Gauss-Jordan method.
, by Gauss-Jordan method.
Solution
Applying Gauss-Jordan method, we get
Example 1.21
Find the inverse of A = 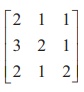 by Gauss-Jordan method.
by Gauss-Jordan method.
Solution
Applying Gauss-Jordan method, we get

Related Topics