Matrix: Gaussian Elimination Method

Gaussian Elimination Method

This method can be applied even if the coefficient matrix is singular matrix and rectangular matrix. It is essentially the method of substitution which we have already seen. In this method, we transform the augmented matrix of the system of linear equations into row-echelon form and then by back-substitution, we get the solution.

Example 1.27

Solve the following system of linear equations, by Gaussian elimination method :

4x + 3y + 6z = 25, x + 5 y + 7z = 13, 2x + 9 y + z = 1.

Solution

Transforming the augmented matrix to echelon form, we get

The equivalent system is written by using the echelon form:

 x + 5y  + 7z = 13 , … (1)

 17y + 22z = 27 , … (2)

 199z = 398 . … (3)

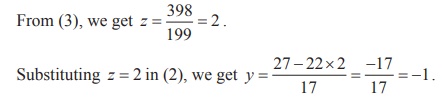
Substituting z = 2, y = -1  in (1), we get x = 13 - 5  × (−1 ) − 7 × 2 = 4 .

So, the solution is ( x =4, y = - 1, z = 2 ).

Note. The above method of going from the last equation to the first equation is called the method of back substitution.

Example 1.28

The  upward  speed  v(t) of a rocket  at time t is approximated by v(t) = at² + bt + c, 0 ≤  t ≤ 100 where a, b, and c are constants. It has been found that the speed at times t = 3, t = 6 , and t = 9 seconds are respectively, 64, 133, and 208 miles per second respectively. Find the speed at time  t = 15 seconds. (Use Gaussian elimination method.)

Solution

Since v(3) =64, v(6) = 133 and v(9) = 208 , we get the following system of linear equations

 9a +3b + c = 64 ,

 36a + 6b + c = 133,

 81a + 9b + c = 208 .

We solve the above system of linear equations by Gaussian elimination method.

Reducing the augmented matrix to an equivalent row-echelon form by using elementary row  operations, we get

Writing the equivalent equations from the row-echelon matrix, we get

9a + 3b + c =  64, 2b + c = 41, c= 1.

By back substitution, we get 

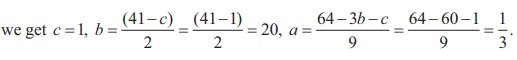
So, we get v (t) = 1/3 t²  + 20t + 1.

Hence, v(15) = 1/3 (225) + 20(15) + 1 = 75 + 300 + 1 = 376