Chapter: 12th Mathematics : UNIT 1 : Applications of Matrices and Determinants
Inverse of a Non-Singular Square Matrix: Solved Example Problems
Example 1.1
If A = 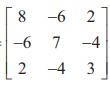 , verify that A (adj A) = (adj A) A = | A | I3 .
, verify that A (adj A) = (adj A) A = | A | I3 .
Solution

Example 1.2
If A = 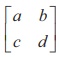 is non-singular, find AŌłÆ1
is non-singular, find AŌłÆ1
Solution
We first find adj A. By definition, we get
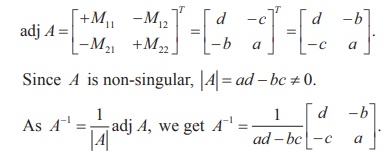
Example 1.3
Find the inverse of the matrix 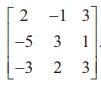
Solution
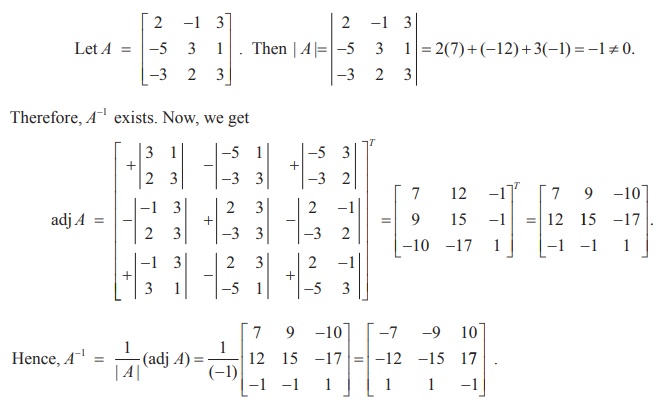
Example 1.4
If A is a non-singular matrix of odd order, prove that |adj A| is positive.
Solution
Let A be a non-singular matrix of order 2m + 1 , where m = 0,1, 2, .. . . Then, we get |A| ŌēĀ 0 and, by theorem 1.9 (ii), we have |adj A| = |A|(2m+1)-1 = |A|2m
Since |A|2m is always positive, we get that |adj A| is positive.
Example 1.5
Find a matrix A if adj( A) = 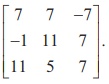
Solution
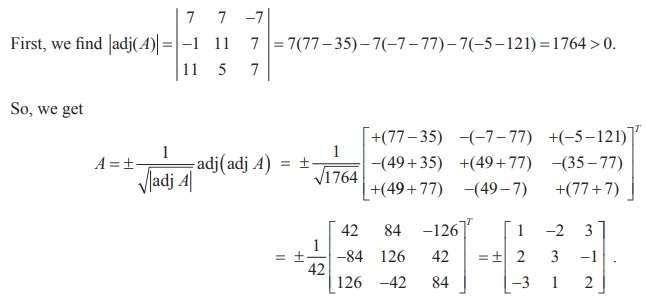
Example 1.6
If adj A =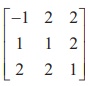 find AŌłÆ1.
find AŌłÆ1.
Solution
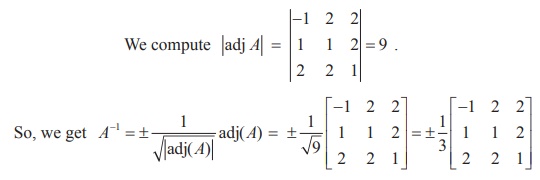
Example1.7
If A is symmetric, prove that adj A is also symmetric.
Solution
Suppose A is symmetric. Then, AT = A and so, by theorem 1.9 (vi), we get
adj (AT) = (adj A) T ŌćÆ adj A = (adj A)T ŌćÆ adj A is symmetric
Example 1.8
Verify the property ( AT )ŌłÆ1 = ( AŌłÆ1 )T with A = 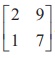 .
.
Solution
For the given A, we get |A |= (2) (7) - (9)(1) = 14 ŌłÆ 9 = 5 .
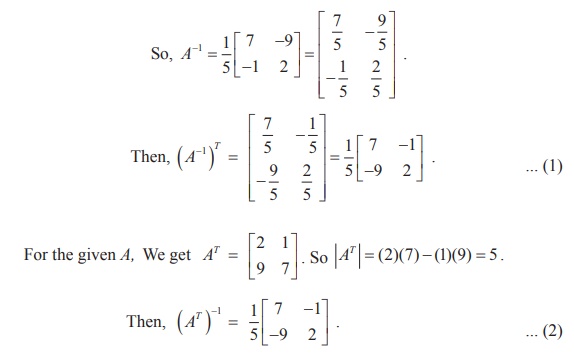
From (1) and (2), we get (A-1) = (AT)-1. Thus, we have verified the given property.
Example 1.9
Verify ( AB)ŌłÆ1 = BŌłÆ1 AŌłÆ1 with 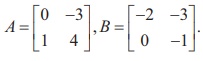
Solution
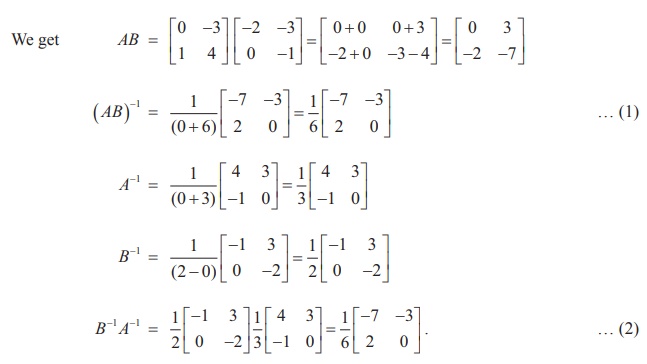
As the matrices in (1) and (2) are same, (AB) ŌłÆ1 = B-1 A-1 is verified.
Example 1.10
If A = 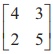 , find x and y such that A2 + xA + yI2=O2, Hence, find AŌłÆ1.
, find x and y such that A2 + xA + yI2=O2, Hence, find AŌłÆ1.
Solution
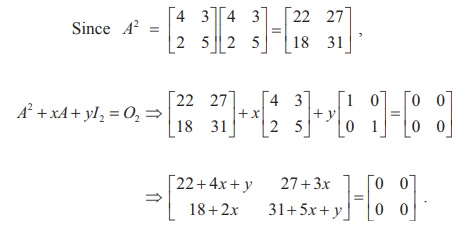
So, we get 22 + 4x + y =0, 31+5x+y=0, 27+3x=0 and 18+2x=0
Hence x = ŌłÆ9 and y =14.Then, we get A2 - 9A + 14I2 = O2
Post-multiplying this equation by AŌłÆ1 , we get A ŌĆō 9I2 + 14A-1 = O2. Hence, we get
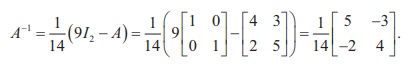
Example 1.11
Prove that 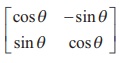 is orthogonal.
is orthogonal.
Solution
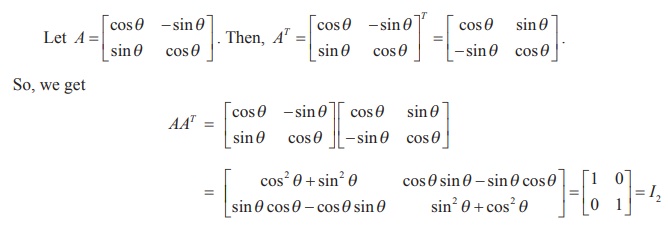
Similarly, we get ATA = I2 . Hence AAT = ATA = I2 ŌćÆ A is orthogonal.
Example 1.12
If A = 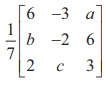 , is orthogonal, find a, b and c , and hence AŌłÆ1.
, is orthogonal, find a, b and c , and hence AŌłÆ1.
Solution
If A is orthogonal, then AAT = AT A = I3 . So, we have
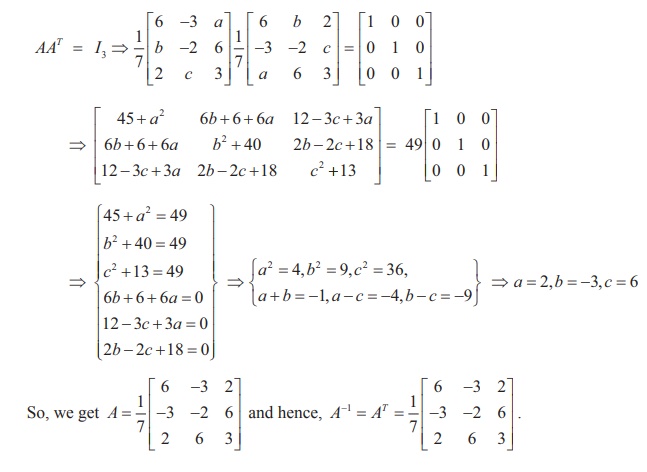
Related Topics