Applications of Matrices and Determinants - Choose the Correct Answers | 12th Mathematics : UNIT 1 : Applications of Matrices and Determinants
Chapter: 12th Mathematics : UNIT 1 : Applications of Matrices and Determinants
Choose the Correct Answers
Choose the Correct or the most suitable answer from the given four alternatives:
1. If | adj(adj A) |=| A |9 , then the order of the square matrix A is
(1) 3
(2) 4
(3) 2
(4) 5

2. If A is a 3├Ś 3 non-singular matrix such that AAT = AT A and B = AŌłÆ1 AT , then BBT =
(1) A
(2) B
(3) I3
(4) BT

3. If A = 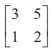 , B = adj A and C = 3A , then | adj B | / |C| =
, B = adj A and C = 3A , then | adj B | / |C| =
(1) 1/3
(2) 1/9
(3) 1/4
(4) 1

4. if 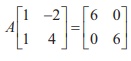 , then A =
, then A =
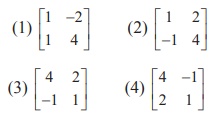
Ans: (3)

5. if  , then 9I2 ŌĆō A =
, then 9I2 ŌĆō A =
(1) A-1
(2) A-1/2
(3) 3A-1
(4) 2A-1

6. if 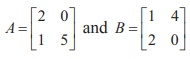 then | adj ( AB) |=
then | adj ( AB) |=
(1) -40
(2) -80
(3) -60
(4) -20

7. If P= 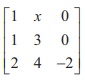 is the adjoint of 3├Ś 3 matrix A and | A |= 4 , then x is
is the adjoint of 3├Ś 3 matrix A and | A |= 4 , then x is
(1) 15
(2) 12
(3) 14
(4) 11

8.If A= 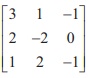 , and AŌłÆ1 =
, and AŌłÆ1 = 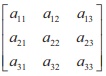 then the value of a23 is
then the value of a23 is
(1) 0
(2) -2
(3) -3
(4) -1

9. If A, B and C are invertible matrices of some order, then which one of the following is not true?
(1) adj A =| A | A-1
(2) adj( AB) = (adj A)(adj B)
(3) det A-1 = (det A)-1
(4) ( ABC)-1 = C-1B-1A-1

10. If ( AB)ŌłÆ1 = 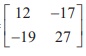 , and A-1 =
, and A-1 = 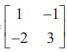 , then BŌłÆ1 =
, then BŌłÆ1 =
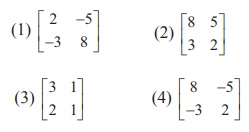
Ans: (1)

11. If AT AŌłÆ1 is symmetric, then A2 =
(1) A-1
(2) (AT)2
(3) AT
(4) ( A-1 )2

12. If A is a non-singular matrix such that AŌłÆ1 = 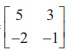 , then ( AT )ŌłÆ1 =
, then ( AT )ŌłÆ1 =
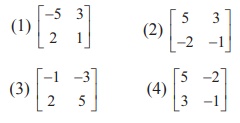
Ans: (4)

13.if A=  , and AT = AŌłÆ1 , then the value of x is
, and AT = AŌłÆ1 , then the value of x is
(1) -4/5
(2) -3/5
(3) 3/5
(4) 4/5
Ans: (1)

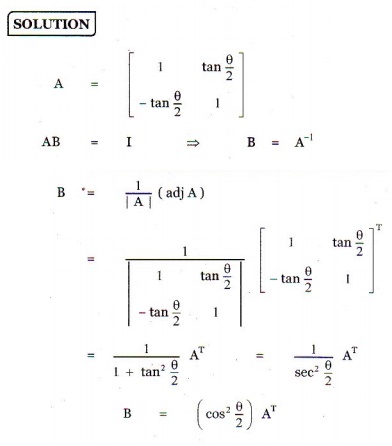
14.if A= 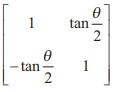 , and AB = I2 , then B=
, and AB = I2 , then B=
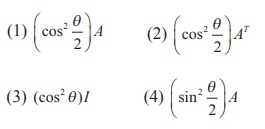
Ans: (2)
15. if A= 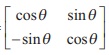 , and A(adj A) =
, and A(adj A) = 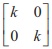 , then k=
, then k=
(1) 0
(2) sin╬Ė
(3) cos╬Ė
(4) 1
Ans: (4)

16. If A= 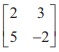 , be such that ╬╗ AŌłÆ1 = A , then ╬╗ is
, be such that ╬╗ AŌłÆ1 = A , then ╬╗ is
(1) 17
(2) 14
(3) 19
(4) 21

17.If adj A= 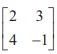 , adj B=
, adj B= 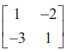 , then adj ( AB) is
, then adj ( AB) is
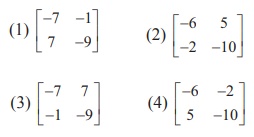
Ans: (2)

18. The rank of the matrix  is
is
(1) 1
(2) 2
(3) 4
(4) 3
Ans: (1)

19. If xa yb = em , xc yd = en , 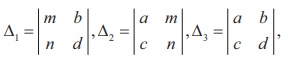 then the values of x and y are respectively,
then the values of x and y are respectively,
(1) e(Δ2 / Δ1 ) , e(Δ3 / Δ1 )
(2) log(Δ1/ Δ3 ), log(Δ2/Δ3)
(3) log(Δ2/ Δ1 ), log(Δ3/Δ1)
(4) ) e(Δ1 / Δ3 ) ,e(Δ2/Δ3 )

20. Which of the following is/are correct?
(i) Adjoint of a symmetric matrix is also a symmetric matrix.
(ii) Adjoint of a diagonal matrix is also a diagonal matrix.
(iii) If A is a square matrix of order n and ╬╗ is a scalar, then adj( ╬╗ A) = ╬╗n adj( A) .
(iv) A(adjA) = (adjA) A =| A | I
(1) Only (i)
(2) (ii) and (iii)
(3) (iii) and (iv)
(4) (i), (ii) and (iv)

21. If Žü ( A) = Žü ([ A | B]) , then the system AX = B of linear equations is
(1) consistent and has a unique solution
(2) consistent
(3) consistent and has infinitely many solution
(4) inconsistent

22. If 0 Ōēż ╬Ė Ōēż ŽĆ and the system of equations x + (sin╬Ė ) y ŌłÆ (cos╬Ė )z = 0, (cos╬Ė )x ŌłÆ y + z = 0, (sin╬Ė )x + y ŌłÆ z = 0 has a non-trivial solution then ╬Ė is
(1) 2ŽĆ/3
(2) 3ŽĆ/4
(3) 5ŽĆ/6
(4) ŽĆ/4

23. The augmented matrix of a system of linear equations is  . The system has infinitely many solutions if
. The system has infinitely many solutions if
(1) ╬╗ = 7, ╬╝ ŌēĀ -5
(2) ╬╗ = -7, ╬╝ = 5
(3) ╬╗ ŌēĀ 7, ╬╝ ŌēĀ -5
(4) ╬╗ = 7, ╬╝ = -5

24. let A = 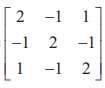 , and 4B =
, and 4B = 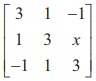 , If B is the inverse of A , then the value of x is
, If B is the inverse of A , then the value of x is
(1) 2
(2) 4
(3) 3
(4) 1

25.If A=  , then adj(adj A) is
, then adj(adj A) is
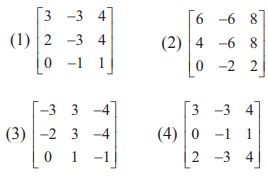
Ans: (1)
Choose the Correct or the most suitable answer from the given four alternatives:
1. If | adj(adj A) |=| A |9 , then the order of the square matrix A is
(1) 3
(2) 4
(3) 2
(4) 5
2. If A is a 3├Ś 3 non-singular matrix such that AAT = AT A and B = AŌłÆ1 AT , then BBT =
(1) A
(2) B
(3) I3
(4) BT
3. If A = 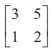 , B = adj A and C = 3A , then | adj B | / |C| =
, B = adj A and C = 3A , then | adj B | / |C| =
(1) 1/3
(2) 1/9
(3) 1/4
(4) 1
4. if 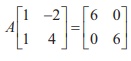 , then A =
, then A =
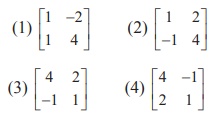
Ans: (3)
5. if  , then 9I2 ŌĆō A =
, then 9I2 ŌĆō A =
(1) A-1
(2) A-1/2
(3) 3A-1
(4) 2A-1
6. if 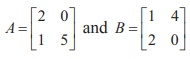 then | adj ( AB) |=
then | adj ( AB) |=
(1) -40
(2) -80
(3) -60
(4) -20
7. If P= 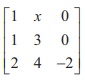 is the adjoint of 3├Ś 3 matrix A and | A |= 4 , then x is
is the adjoint of 3├Ś 3 matrix A and | A |= 4 , then x is
(1) 15
(2) 12
(3) 14
(4) 11
8.If A= 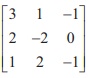 , and AŌłÆ1 =
, and AŌłÆ1 = 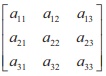 then the value of a23 is
then the value of a23 is
(1) 0
(2) -2
(3) -3
(4) -1
9. If A, B and C are invertible matrices of some order, then which one of the following is not true?
(1) adj A =| A | A-1
(2) adj( AB) = (adj A)(adj B)
(3) det A-1 = (det A)-1
(4) ( ABC)-1 = C-1B-1A-1
10. If ( AB)ŌłÆ1 = 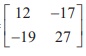 , and A-1 =
, and A-1 = 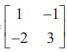 , then BŌłÆ1 =
, then BŌłÆ1 =
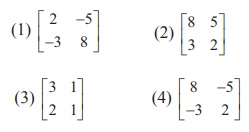
Ans: (1)
11. If AT AŌłÆ1 is symmetric, then A2 =
(1) A-1
(2) (AT)2
(3) AT
(4) ( A-1 )2
12. If A is a non-singular matrix such that AŌłÆ1 = 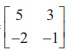 , then ( AT )ŌłÆ1 =
, then ( AT )ŌłÆ1 =
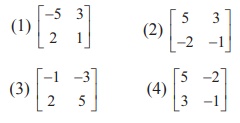
Ans: (4)
13.if A=  , and AT = AŌłÆ1 , then the value of x is
, and AT = AŌłÆ1 , then the value of x is
(1) -4/5
(2) -3/5
(3) 3/5
(4) 4/5
Ans: (1)
14.if A= 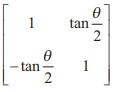 , and AB = I2 , then B=
, and AB = I2 , then B=
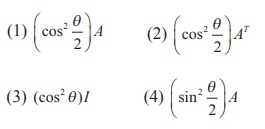
Ans: (2)
15. if A= 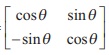 , and A(adj A) =
, and A(adj A) = 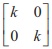 , then k=
, then k=
(1) 0
(2) sin╬Ė
(3) cos╬Ė
(4) 1
Ans: (4)
16. If A= 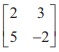 , be such that ╬╗ AŌłÆ1 = A , then ╬╗ is
, be such that ╬╗ AŌłÆ1 = A , then ╬╗ is
(1) 17
(2) 14
(3) 19
(4) 21
17.If adj A= 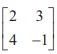 , adj B=
, adj B= 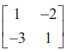 , then adj ( AB) is
, then adj ( AB) is
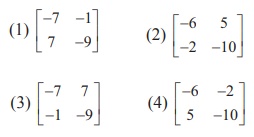
Ans: (2)
18. The rank of the matrix  is
is
(1) 1
(2) 2
(3) 4
(4) 3
Ans: (1)
19. If xa yb = em , xc yd = en , 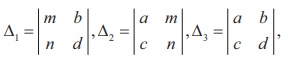 then the values of x and y are respectively,
then the values of x and y are respectively,
(1) e(Δ2 / Δ1 ) , e(Δ3 / Δ1 )
(2) log(Δ1/ Δ3 ), log(Δ2/Δ3)
(3) log(Δ2/ Δ1 ), log(Δ3/Δ1)
(4) ) e(Δ1 / Δ3 ) ,e(Δ2/Δ3 )
20. Which of the following is/are correct?
(i) Adjoint of a symmetric matrix is also a symmetric matrix.
(ii) Adjoint of a diagonal matrix is also a diagonal matrix.
(iii) If A is a square matrix of order n and ╬╗ is a scalar, then adj( ╬╗ A) = ╬╗n adj( A) .
(iv) A(adjA) = (adjA) A =| A | I
(1) Only (i)
(2) (ii) and (iii)
(3) (iii) and (iv)
(4) (i), (ii) and (iv)
21. If Žü ( A) = Žü ([ A | B]) , then the system AX = B of linear equations is
(1) consistent and has a unique solution
(2) consistent
(3) consistent and has infinitely many solution
(4) inconsistent
22. If 0 Ōēż ╬Ė Ōēż ŽĆ and the system of equations x + (sin╬Ė ) y ŌłÆ (cos╬Ė )z = 0, (cos╬Ė )x ŌłÆ y + z = 0, (sin╬Ė )x + y ŌłÆ z = 0 has a non-trivial solution then ╬Ė is
(1) 2ŽĆ/3
(2) 3ŽĆ/4
(3) 5ŽĆ/6
(4) ŽĆ/4
23. The augmented matrix of a system of linear equations is  . The system has infinitely many solutions if
. The system has infinitely many solutions if
(1) ╬╗ = 7, ╬╝ ŌēĀ -5
(2) ╬╗ = -7, ╬╝ = 5
(3) ╬╗ ŌēĀ 7, ╬╝ ŌēĀ -5
(4) ╬╗ = 7, ╬╝ = -5
24. let A = 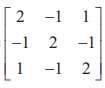 , and 4B =
, and 4B = 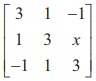 , If B is the inverse of A , then the value of x is
, If B is the inverse of A , then the value of x is
(1) 2
(2) 4
(3) 3
(4) 1
25.If A=  , then adj(adj A) is
, then adj(adj A) is
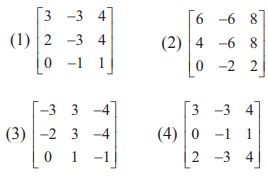
Ans: (1)
Related Topics