Chapter: 11th Chemistry : UNIT 7 : Thermodynamics
Various statements of the second law of thermodynamics
Various statements of the second law of thermodynamics
Entropy
The second law of thermodynamics introduces another state function called entropy. Entropy is a measure of the molecular disorder (randomness) of a system. But thermodynamic definition of entropy is concerned with the change in entropy that occurs as a result of a process.
It is defined as, dS = dqrev / T
Entropy statement:
The second law of thermodynamics can be expressed in terms of entropy. i.e ŌĆ£the entropy of an isolated system increases during a spontaneous processŌĆØ.
For an irreversible process such as spontaneous expansion of a gas,
ŌłåStotal > 0
ŌłåStotal > ŌłåSsystem + ŌłåSsurrounding
i.e. ŌłåSuniverse > ŌłåSsystem + ŌłåSsurrounding
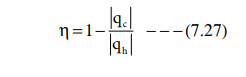
For a reversible process such as melting of ice,
ŌłåSsystem = - ŌłåSsurrounding
ŌłåSuniverse = 0
Kelvin-Planck statement:
It is impossible to construct a machine that absorbs heat from a hot source and converts it completely into work by a cyclic process without transferring a part of heat to a cold sink. The second law of thermodynamics explains why even an ideal, frictionless engine cannot convert 100% of its input heat into work. Carnot on his analysis of heat engines, found that the maximum efficiency of a heat engine which operates reversibly, depends only on the two temperatures between which it is operated.
Efficiency = work performed / heat absorbed
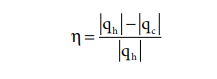
qh - heat absorbed from the hot reservoir
qc - heat transferred to cold reservoir
For a reversible cyclic process
ΔSuniverse = ΔSsystem + ΔSsurroundings = 0
ΔSsystem = - ΔSsurroundings
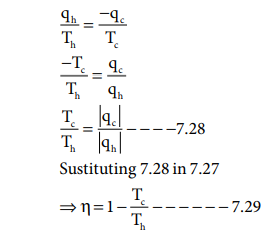
Th >> Tc
Hence, ╬Ę < 1
efficiency in percentage can be expressed as
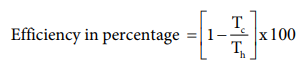
Clausius statement:
It is impossible to transfer heat from a cold reservoir to a hot reservoir without doing some work.
Problem: 7.10
If an automobile engine burns petrol at a temperature of 816o C and if the surrounding temperature is 21o C, calculate its maximum possible efficiency.
Solution:
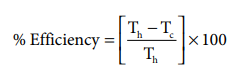
Here
Th = 816+273= 1089 K;
Tc= 21+273= 294K
%Efficiency=( 1089-294 / 1089) x100
%Efficiency=73%
Unit of entropy:
The entropy (S) is equal to heat energy exchanged (q) divided by the temperature (T) at which the exchange takes place. Therefore, The SI unit of entropy is JKŌłÆ1.
Spontaneity and Randomness
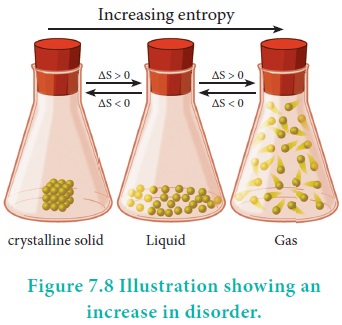
Careful examination shows that in each of the processes viz., melting of ice and evaporation of water, there is an increase in randomness or disorder of the system. The water molecules in ice are arranged in a highly organised crystal pattern which permits little movement. As the ice melts, the water molecules become disorganised and can move more freely. The movement of molecules becomes freer in the liquid phase and even more free in the vapour phase. In other words, we can say that the randomness of the water molecules increases, as ice melts into water or water evaporates. Both are spontaneous processes which result in a increase in randomness (entropy).
Standard Entropy Change(ΔS0):
It is possible to calculate the actual entropy of a substance at any temperature above 0 K. The absolute entropy of a substance at 298 K and one bar pressure is called the standard entropy So. The third law of thermodynamics states, according to Nernst, that the absolute entropy of elements is zero only at 0 K in a perfect crystal, and standard entropies of all substances at any temperature above 0 K always have positive values. Once we know the entropies of different substances, we can calculate the standard entropy change ( Sr0 ) for chemical reactions.
S0r = Ōłæ S0products ŌłÆ Ōłæ Sreac0 tan ts ------- (7.30)
Standard Entropy of Formation:
Standard entropy of formation is defined as ŌĆ£the entropy of formation of 1 mole of a compound from the elements under standard conditionsŌĆØ. It is denoted as ŌłåS0f . We can calculate the value of entropy of a given compound from the values of S0 of elements.
Problem: 7.6
Calculate the standard entropy change for the following reaction( ŌłåS0f ), given the standard entropies of CO2(g), C(s),O2(g) as 213.6 , 5.740 and 205 JKŌłÆ1 respectively.
C(g) + O2(g) ŌåÆCO2(g)
S0r = Ōłæ S0products ŌłÆ Ōłæ Sreac0 tan ts
S0r = {S0CO 2 } ŌłÆ {SC0 + S0O2 }
S0r = 213.6 ŌłÆ [5.74 + 205]
S0r = 213.6 ŌłÆ[210.74]
S0r = 2.86 JKŌłÆ1
Entropy change accompanying change of phase
When there is a change of state from solid to liquid (melting), liquid to vapour (evaporation) or solid to vapour (sublimation) there is a change in entropy. This change may be carried out at constant temperature reversibly as two phases are in equilibrium during the change.
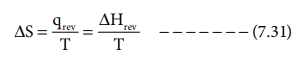
Entropy of fusion:
The heat absorbed, when one mole of a solid melts at its melting point reversibly, is called molar heat of fusion. The entropy change for this process is given by

where ΔHfusion is Molar heat of fusion. Tf is the melting point.
Entropy of vapourisation:
The heat absorbed, when one mole of liquid is boiled at its boiling point reversibly, is called molar heat of vapourisation. The entropy change is given by

where ΔHv is Molar heat of vaporisation.
Tb is the boiling point.
Entropy of transition:
The heat change, when one mole of a solid changes reversibly from one allotropic form to another at its transition temperature is called enthalpy of transition. The entropy change is given
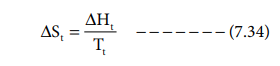
where ΔHt is the molar heat of transition, Tt is the transition temperature.
Problem: 7.7
Calculate the entropy change during the melting of one mole of ice into water at 00 C and 1 atm pressure. Enthalpy of fusion of ice is 6008 J mol-1
Given:
ŌłåHfusion = 6008 JmolŌłÆ1
Tf = 0 0
C = 273 K
H 2O(S) --273 KŌåÆ H 2O ( l)

S fusion = 22 .007 J K ŌłÆ1 moleŌłÆ1
Related Topics