Chapter: 11th Chemistry : UNIT 7 : Thermodynamics
Brief Questions and Answers: Thermodynamics
Thermodynamics | Chemistry
Answer the following questions
26. State the first law of thermodynamics.
"Energy
can neither be created nor destroyed, but may be converted from one form to
another"
27. Define Hess's law of constant heat summation.
The
enthalpy change of a reaction either at constant volume or constant pressure is
the same whether it takes place in a single or multiple steps.
28. Explain intensive properties with two examples
Intensive
properties are the properties that is independent of the mass or size of the
system.
Example
:
Temperature and boiling point.
29. Define the following terms:
a. isothermal process
b. adiabatic process
c. isobaric process
d. isochoric process
a.
Isothermal process is defined as one in which the temperature of the system
remains constant, during the change from its initial to final states. ie., dT =
0
b.
The process in which no heat can flow into or out of the system is called
adiabatic process ie., q = 0
c.
Isobaric process is defined as one in which the Pressure of the system remains
constant during its change from the initial to final state ie., dp = 0
d.
Isochoric process is defined as one in which the volume of system remains
constant during its change from initial to final state of the process, i.e., dv
= 0
30. What is the usual definition of entropy? What is the unit of entropy?
Entropy
is a measure of randomness or disorderliness of the system. Entropy (s) is
equal to heat energy (q) divided by constant temperature.
S = q/T
UNITS
OF ENTROPY : SI Unit: JKŌłÆ1
CGS
Unit: cal KŌłÆ1
31. Predict the feasibility of a reaction when
i) both ΔH and ΔS positive
ii) both ΔH and ΔS negative
iii) ΔH decreases but ΔS increases
i)
when both ╬öH and ╬öS are positive, then ╬öG to be ŌłÆve only reaction is carried
out at high temperature it is feasible.
In
otherwords, TΔS > ΔH, then the reaction is feasible.
ii)
When both ╬öH and ╬öS are negative, then ╬öG to be ŌłÆve only if reaction is carried
out at low temperature is, it is feasible. In other words,
TΔS
< ΔH, then the reaction is feasible.
iii)
When ╬öH is ŌłÆve but ╬öS is +ve, the ╬öG becomes ŌłÆve is feasible at constant
temperature.
32. Define is GibbŌĆÖs free energy.
"Gibbs
free energy is defined as the part of the total energy of a system that can be
converted (or) available for conversion into work".
G
is mathematically defined as G =H ŌłÆ TS When H ŌłÆ enthalpy, T- temperature, S ŌłÆ entropy.
33. Define enthalpy of combustion.
Enthalpy
of combustion of a substance is defined as "The change in enthalpy of a
system when one mole of the substance is completely burnt in excess of air or
oxygen". It is denoted by ΔHC.
34. Define molar heat capacity. Give its unit.
The
molar heat capacity may be defined as " The amount of heat absorbed by one
mole of the substance to raise in temperature by 1 kelvin"
Unit
: JKŌłÆ1 molŌłÆ1 (SI)
35. Define the calorific value of food. What is the unit of calorific value?
The
Calorific value of food is defined as :
The
amount of heat produced in calories (or joules) when one gram of a food is
completely burnt. It is expressed in cal g ŌłÆ1. In SI unit it is
expressed in J Kg ŌłÆ1
36. Define enthalpy of neutralization.
The
enthalpy of neutralizations is defined as "The change in enthalpy of the
system when one gram equivalent of an acid is neutralised by one gram
equivalent of a base or vice versa in dilute solution".
37. What is lattice energy?
Lattice
energy is defined as the amount of energy required to completely separate one
mole of a solid ionic compound into gaseous constituent. It is also referred as
lattice enthalpy.
38. What are state and path functions? Give two examples.
State
functions:
The
variables like P,V,T and 'n' that are used to describe the state of a system
are called as state functions. A state function is a thermodynamic property of
a system, which has a specific value for each state of the system and does not
depend on the path (or manner ) in which a particular state is reached.
Example:
Pressure(P), Volume (V), Temperature (T), Internal energy(U), Enthalpy (H),
free energy (G) etc.
Path
functions:
A
path function is a thermodynamic property of the system whose value depends on
the path or manner by which the system goes from its initial to final states. Example:
Work (w), Heat (q).
39. Give Kelvin statement of second law of thermodynamics.
It
is impossible to take heat from a hotter reservoir and convert it completely
into work by a cyclic process without transferring a part of heat to a cooler
reservoir.
40. The equilibrium constant of a reaction is 10, what will be the sign of ŌłåG? Will this reaction be spontaneous?
We
know that, ╬öG = ŌłÆ2.303RT log K
= ŌłÆ2.303 RT log l0
ΔG
= ŌłÆ2.303RT [log 10 =1]
since,
╬öG is ŌłÆve, the reaction is spontaneous.
41. Enthalpy of neutralization is always a constant when a strong acid is neutralized by a strong base: account for the statement.
According
to Arrhenius theory of electroytic dissociation, strong acid and strong base
ionizes completely in dilute solution to produce H+ ions and OHŌłÆ
ions respectively results in neutralisation to give net reaction water. Hence,
enthalpy of neutralisation of strong acid and strong base is always a constant
ie., 57.32 kJ
H+(aq)
+ OHŌłÆ (aq) ŌåÆ H2O(l) ╬öH = -57.32 KJ
42. State the third law of thermodynamics.
The
third law of the thermodynamics states that the entropy of pure crystalline
substance at absolute zero is zero (or) otherwise it can be states as " it
is impossible to lower the temperature of an object to absolute zero in a
finite number of steps. Mathematically
lim T ŌåÆ 0 S
= 0
43. Write down the Born-Haber cycle for the formation of CaCl2
Born
- Haber cycle for the formation of CaCl2 as follows:

According
to Hess's law of constant heat of summation;
ΔHf
= ΔH4 + ΔH2 + ΔH3 + 2ΔH4 + U
Where
ΔHf = Enthalpy change for formation of CaCl2
ΔH1
= Enthalpy change for sublimation
ΔH2
= Enthalpy change for dissociation
ΔH3
= Ionisation Energy
ΔH4
= Electron Affinity
U
= Lattice enthalpy for formation of CaCl2.
44. Identify the state and path functions out of the following: a)Enthalpy b)Entropy c) Heat d) Tem-perature e) Work f)Free energy.
State
Funtion
Enthalpy
:
Entropy
Temperature
Free
Energy
Path
Funciton
Heat
Work
45. State the various statements of second law of thermodynamics.
1.
Entropy statements:
"whenever
a spontaneous process takes place, it is accompanied by an increase in the
total entropy of the Universe".
2.
Kelvin - planck statement:
It
is impossible to take heat from hotter reservoir and convert it completely into
work by a cyclic process without transferring a part of heat to a cooler
reservoir.
3.
Clausius statement:
Heat
flows spontaneously from hot objects to cold objects and to get it flow in the
opposite direction, we have to expend some work.
46. What are spontaneous reactions? What are the conditions for the spontaneity of a process?
A
reaction which takes place on their own accord without proper initiation is
called spontaneous reaction. All natural process are spontaneous.
The
necessary condition for a reaction to be spontaneous is ╬ö H ŌĆōT╬öS < 0, then
only ΔG will be negative.
47. List the characteristics of internal energy.
ŌŚÅ
Characteristics of internal energy (U):
Internal
energy of a system is an extensive property. It depends on the amount of the
substances present in the system. If the amount is doubled, internal energy is
also doubled.
ŌŚÅ
Internal energy of a system is a state function. It depends only upon the state
variables ( T, P, V, n) of the system. The change in internal energy does not
depend on the path by which the final state is reached.
ŌŚÅ
The change in internal energy of a system is expressed as ╬öU = U2 ŌĆō
U1
ŌŚÅ
In a cyclic process, there is no energy change. ΔU(cyclic) = 0.
ŌŚÅ
If the internal energy of the system at final state ( Uf) is less
than the internal energy of the system at its initial state (Ui),
then ╬öU = Uf ŌłÆ Ui = ŌłÆveUf < Ui
ŌŚÅ
If the internal energy of the system at final state (Uf) is greater
than the internal energy of the system at its initial state (Ui),
then Δ U would be negative.
ΔU
= Uf ŌłÆ Ui = ŌłÆ ve Uf < Ui
48. Explain how heat absorbed at constant volume is measured using bomb calorimeter with a neat diagram.
For
chemical reactions, heat evolved at constant volume, is measured in a bomb
calorimeter.
ŌŚÅ
The inner vessel( the bomb) and its cover are made of strong steel. The cover
is fitted tightly to the vessel by means of metal lid and screws.
ŌŚÅ
A weighted amount of the substance is taken in a platinum cup connected with
electrical wires for striking an arc instantly to kindle combustion. The bomb
is then tightly closed and pressurized with excess oxygen.
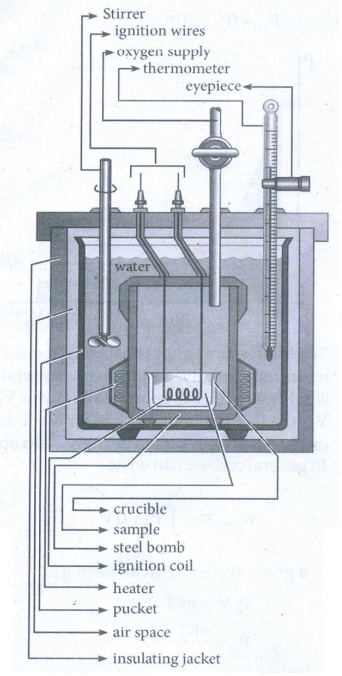
ŌŚÅ
The bomb is lowered in water, which is placed inside the calorimeter. A stirrer
is placed in the space between the wall of the calorimeter and the bomb, so
that water can be stirred, uniformly.
ŌŚÅ
The reaction is started by striking the substance through electrical heating.
ŌŚÅ
A known amount of combustible substance is burnt in oxygen in the bomb. Heat
evolved during the reaction is absorbed by the calorimeter as well as the water
in which the bomb is immersed using a Beckman thermometer.
ŌŚÅ
Since the bomb is sealed its volume does not change and hence the heat
measurements is equal to the heat of combustion at a constant volume (ΔU)c.
ŌŚÅ
The amount of heat produced in the reaction (ΔU)c is equal to the sum of the
heat abosrbed by the calorimeter and the water.
Heat
absorbed by the calorimeter q1 = kΔT where k is a calorimeter
constant equal to mc Cc (mc is mass of the calorimeter and Cc is heat capacity
of calorimeter)
Heat
absorbed by the water q2 = mwCwΔT where mw
is molar mass of water Cw is molar heat capacity of water (4,184 kJ
KŌłÆ1 mol ŌłÆ1)
Therefore
ΔUC = q1 + q2
=
kΔT + mwCwΔT
=
(k + mwCw)ΔT
ŌŚÅ
Calorimeter constant can be determined by burning a known mass of standard sample
(benzoic acid) for which the heat of combustion is known (ŌłÆ3227 kJ molŌłÆ1)
The
enthalpy of combustion at constant pressure of the substance is calculated from
the equation
ΔHCo
(pressure) = ΔUCo (vol) + ΔngRT
49. Calculate the work involved in expansion and compression process.
ŌŚÅ
In most thermodynamic calculations we are dealing with the evaluation of work
involved in the expansion or compression of gases.
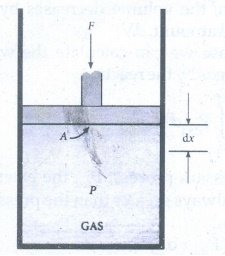
ŌŚÅ
The essential condition for expansion or compression of a system is that there
should be difference between external pressure (Pext) and internal
pressure (Pint).
ŌŚÅ
For understanding pressure volume work, let us consider a cylinder which
contains 'n' moles of an ideal gas fitted with a frictionless piston of cross
sectional area A.
ŌŚÅ
The total volume of the gas inside is Vi and pressure of the gas inside is Pint.
ŌŚÅ
If the external pressure Pext is greater than Pint, the
piston moves inward till the pressure inside becomes equal to Pext.
Let this change be achieved in a single step and the final volume be Vf.
In
this case, the work is done on the system (+ w). It can be calculated as
follows
w
= ŌłÆF. ╬öx ŌĆ”ŌĆ”ŌĆ”ŌĆ”ŌĆ”ŌĆ”ŌĆ”
(1)
where
dx is the distance moved by the piston during the compression and F is the
force action on the gas.
F
= PextA ŌĆ”ŌĆ”ŌĆ”ŌĆ”ŌĆ”ŌĆ”.
(2)
Substituting
(2) in (1)
w
= ŌłÆ PextA. ╬öx
A.Δx
= change in volume = Vf ŌłÆ Vi
w
= ŌłÆPext. (Vf ŌłÆ Vi) ŌĆ”ŌĆ”ŌĆ”ŌĆ”ŌĆ”.. (3)
w
= ŌłÆ Pext. (-╬öV) ŌĆ”ŌĆ”ŌĆ”ŌĆ”ŌĆ”. (4)
=
Pext. ΔV
Since
work is done on the system, it is a positive quantity.
ŌŚÅ
If the pressure is not constant, but changes during the process such that it is
always infinitesimally greater than the pressure of the gas, then, at each
stage of compression, the volume decreases by an infinitesimal amount, dV.
ŌŚÅ
In such a case we can calculate the work done on the gas by the reaction
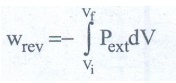
In
a compression process, Pext the external pressure is always greater
than the pressure of the system.
i.e
Pext = (Pint + dP).
In
an expansion process, the external pressure is always less than the pressure of
the system
i.e
Pext = (Pint ŌłÆ dP).

ŌŚÅ
When pressure is not constant and changes in infinitesimally small steps
(reversible conditions) during compression from Vi to Vf,
the P-V plot looks like in fig work done on the gas is represented by the
shaded area. In general case we can write,

For
a given system with an ideal gas
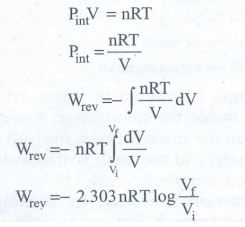
If
Vf >Vi (expansion), the sign of work done by the
process is negative.
If
Vf <Vi (compression) the sign of work done on the
process is positive.
50. Derive the relation between ŌłåH and ŌłåU for an ideal gas. Explain each term involved in the equa-tion.
ŌŚÅ
Consider a closed system of gaseous reactants which are chemically reacting to
produce gaseous products at constant temperature and pressure with Vi
and Vf as the total volumes of gaseous reactants and products
respectively, and nŌĆÖ2 and nf as the number of moles of
gaseous reactants and products, then
Reactants
ŌåÆ products
For
reactants, PVi = ni RT ŌĆ”ŌĆ”ŌĆ”ŌĆ”ŌĆ”.. (1)
For
products PVf = nf RT ŌĆ”ŌĆ”ŌĆ”ŌĆ”ŌĆ”ŌĆ” (2)
(2)
ŌłÆ (1) gives
P(Vf
-Vi) = (nf ŌłÆ ni ) RT
PΔV
= ╬öng RT ŌĆ”ŌĆ”ŌĆ”ŌĆ”ŌĆ” (3)
We
know, ╬öH = ╬öU + P╬öV ŌĆ”ŌĆ”ŌĆ”ŌĆ”.. (4)
Substitute
(3) in (4) we get,
ΔH
= ΔU + Δng RT
Where
ΔH = Enthalpy change at constant pressure
ΔU
= Enthalpy change at constant volume
Δng
= Change in number of moles ( Ōłænpg ŌłÆ Ōłænrg)
R
= Gas constant
T
= Temperature
51. Suggest and explain an indirect method to calculate lattice enthalpy of sodium chloride crystal.
Born
Haber cycle applies Hess's law which is used to calculate lattice enthalpy of
sodium chloride
ŌŚÅ
Let us use the Born - Haber cycle for determining the lattice enthalpy of NaCl
as follows:
ŌŚÅ
Since the reaction is carried out with reactants in elemental forms and
products in their standards states, at 1 bar the overall enthalpy of formation
of NaCl.
ŌŚÅ
Also, the formation of NaCl can be considered in 5 steps.
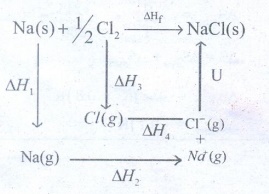
ŌŚÅ
The sum of the enthalpy changes of these steps is equal to the enthalpy changes
for the overall reaction from which the lattice enthalpy of NaCl is calculated.
Let
us calculate the lattice energy of sodium chloride using Born - Haber cycle
ΔHf
= heat of formation of sodium chloride = ŌłÆ411.3 kJ molŌłÆ1
ΔH1
= heat of sublimation of Na(S) = 108.7 kJ moleŌłÆ1
ΔH2
= ionisation energy of Cl2(s) = 495kJ molŌłÆ1
ΔH3
= dissociation energy of Cl2 (s)= 244 kJ molŌłÆ1
ΔH4
= Electron affinity of Cl(s) = ŌłÆ349.0 kJ molŌłÆ1
U
= Lattice energy of NaCl
Δ
Hf = ╬öH1 + ╬öH2 + ┬Į ╬öH3 + ╬öH4
+ U
Ōł┤ U = (╬ö Hf)
ŌłÆ (╬öH1 + ╬öH2 + ┬Į ╬öH3 + ╬öH4)
U
= (ŌłÆ411.3) ŌłÆ (108.7 + 495.0 + 122 ŌłÆ 349)
U
= (ŌłÆ411.3) ŌłÆ (376.7)
Ōł┤ U = ŌłÆ 788
kJ molŌłÆ1
This
negative sign in lattice energy indicates that the energy is released when
sodium is formed from its constituent gaseous ions Na+ and ClŌłÆ.
52. List the characteristics of Gibbs free energy.
1. "Gibbs free energy is
defined as the part of total energy of a system is defined as the part of (or)
available for conversion into Work"
G is mathematically defined as G
= H-Ts
where, H - Energy, T-
Temperature, S - Entropy.
2. G is a state Function and is a
single valued function
3. G is an extensive property,
whereas ΔG becomes intensive property for a closed system. Both G and ΔG Values
correspond to the system only.
4.
╬öG = ╬öH ŌłÆ T╬öS expression is used to predict the spontaneity of a process.
5.
ΔG gives a criteria for spontaneity at constant pressure and temperature.
(i)
If ΔG is negative (ΔG < 0), the process is spontaneous.
(ii)
If ΔG is positive (ΔG > 0), the process is spontaneous.
(iii)
If ΔG = 0 (zero) - process is in equilibrium.
6.
For any system at constant pressure and temperature
The
expression,
ŌłÆ ╬öG = ŌłÆw ŌłÆ P ╬öV = net work
But
ŌłÆP ╬öV represents the work done due to expansion against a constant external
pressure. Therefore, it is clear that the decrease in free energy (ŌłÆ╬öG)
accompanying a process taking place at constant temperature and pressure is
equal to the maximum work obtainable from the system other than the work of
expansion.
7.
Standard free energy of formation of elements are taken as zero.
Related Topics