Evaluate Yourself: Thermodynamics(Chemistry)

Evaluate Yourself

1. Calculate ∆H_f° for the reaction

CO₂(g)+ H₂(g) → CO(g)+ H₂O(g)

given that ∆Hf° for CO₂ (g), CO (g) and H₂O(g) are – 393.5, – 111.31 and – 242 kJ mol–1 respectively.

Solution :

Given

∆H_f⁰ CO₂ = -393.5 kJ mol^-1

∆H_f⁰ CO = -111.31 kJ mol^-1

∆H_f⁰ (H₂O) = -242 kJ mol^-1

CO₂(g) + H₂(g) → CO(g) + H₂O(g)

∆H_r⁰ = ?

∆H_r⁰ = Σ (∆H_f⁰ )_products^{– Σ (∆H}f⁰⁾reactants

∆H_r⁰ = [∆H_f⁰ (CO) + ∆H_f⁰ (H₂O)] – [∆H_f⁰ (CO₂ )+∆H_f⁰

(H₂)] ∆H_r⁰ = [– 111.31 + (– 242)] – [– 393.5 + (0)]

∆H_r⁰ = [– 353.31] + 393.5

∆H_r⁰ = 40.19

∆H_r⁰ = + 40.19 kJ mol^–1

2. Calculate the amount of heat necessary to raise 180 g of water from 25° C to 100° C. Molar heat capacity of water is 75.3 J mol^-1 K^-1

Solution :

Given :

number of moles of water n

=180g / (18g mol^-1  )= 10 mol

molar heat capacity of water

C_P = 75.3 J K^–1 mol^–1

T₂ = 100⁰ C = 373 K

T₁ = 25⁰ C= 298 K

ΔH = nC_P (T₂ – T₁)

 Î”H = 10 mol × 75.3 J mol–1 K–1 × (373 – 298) K

 Î”H = 56475 J

 Î”H = 56.475 kJ

3. From the following data at constant volume for combustion of benzene, calculate the heat of this reaction at constant pressure condition.

C₆H₆(l) + 7½ O₂(g) → 6CO₂ (g) + 3 H₂O(l)

ΔU at 25° C = -3268.12 kJ

Solution :

T = 250 C = 298 K ;

       âˆ†U = –3268.12 kJ mol_–1

       âˆ†H = ?

       âˆ†H = ∆U + ∆n_gRT

       âˆ†H = ∆U + (n_p – n_r) RT

      H = -3268.12+ (6 - 7/2) x 8 314 × 10  -3 x 298.

       âˆ†U = –3268.12  + (2.5 × 8.314 ×10-3 × 298)

       âˆ†U = – 3268.12 + 6.19

       âˆ†U = – 3261.93 kJ mol^–1

4. When a mole of magnesium bromide is prepared from 1 mole of magnesium

and 1 mole of liquid bromine, 524 kJ of energy is released.

The heat of sublimation of Mg metal is 148 kJ mol^–1. The heat of dissociation of bromine gas into atoms is 193 kJ mol^–1. The heat of vapourisation of liquid bromine is 31 kJ mol^–1. The ionisation energy of magnesium is 2187 kJ mol^–1 and the electron affinity of bromine is – 662 kJ mol^–1. Calculate the lattice energy of magnesium bromide.

Solution :

Given :

Mg(S) + Br₂(1) →

MgBr₂(S) ∆H_f⁰ = –524 KJ mol^–1

Sublimation :

Mg(S) → Mg(g)

∆H₁⁰ = +148 KJ mol^–1

Ionisation:

Mg(g) → Mg²⁺(g) + 2e^–

∆H₂⁰ = 2187 KJ mol^–1

Br₂(1) → Br₂(g)

∆H₃⁰ = +31 KJ mol^–1

Dissociation :

Br₂(g) → 2Br(g)

∆H₄⁰ = +193 KJ mol^–1

Electron affinity:

Br(g) + e ^– → Br ^– (g)

∆H₅⁰ = – 331 KJ mol^–1

Solution :

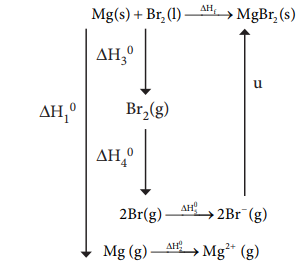
ΔH_f  =ΔH₁ + ΔH₂ + ΔH₃ + ΔH₄ +2ΔH₅ + u

– 524 =   148 + 2187 + 31 + 193+(2 × – 331) + u

– 524 =   1897 + u

u =–524 – 1897

u =– 2421 kJ mol^–1

5. An engine operating between 127⁰ C and 47⁰ C takes some specified amount of heat from a high temperature reservoir. Assuming that there are no frictional losses, calculate the percentage efficiency of an engine.

Solution:

Given

T_h = 127⁰ C = 127 + 273 = 400

K T_C = 47⁰ C = 47 + 273 = 320

K % efficiency η = ?

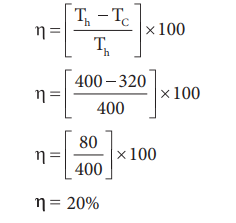
6. Urea on hydrolysis produces ammonia and carbon dioxide. The standard entropies of urea, H₂O, CO₂, NH₃ are 173.8, 70, 213.5 and 192.5J mole^-1K^-1 respectively. Calculate the entropy change for this reaction.

Solution:

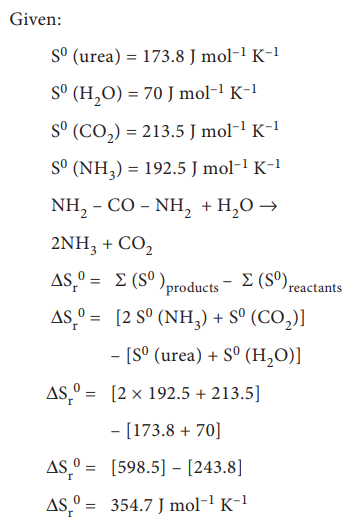
7. Calculate the entropy change when 1 mole of ethanol is evaporated at 351 K. The molar heat of vaporisation of ethanol is 39.84 kJ mol^-1

Solution:

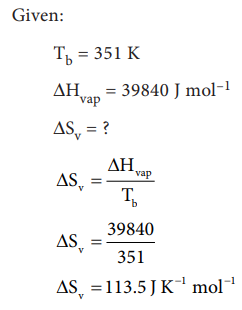
8. For a chemical reaction the values of ΔH and ΔS at 300K are − 10 kJ mole^−1 and −20 J deg^−1 mole^−1 respectively. What is the value of ΔG of the reaction? Calculate the ΔG of a reaction at 600 K assuming ΔH and ΔS values are constant. Predict the nature of the reaction.

Solution:

Given:

ΔH = –10 kJ mol^–1 = –10000 J mol^–1

ΔS = – 20 J K^–1 mol^–1

T =300 K

ΔG =?

ΔG =ΔH – TΔS

ΔG = – 10 kJ mol^–1 – 300 K × (–20x10^-3) kJ K^–1 mol^–1

ΔG =(–10+6) kJ mol^–1

ΔG =– 4 kJ mol^–1

At 600 K

ΔG =– 10 kJ mol^–1 – 600 K

(–20x10^-3) kJ K^–1 mol^–1

ΔG = (–10 + 12) kJ mol^–1

ΔG = + 2 kJ mol^–1

The value of ∆G is negative at 300K and the reaction is spontaneous, but at 600K the value ∆G becomes positive and the reaction is non spontaneous.