Gibbs free energy (G)

Gibbs free energy (G)

One of the important applications of the second law of thermodynamics is to predict the spontaneity of a reaction under a specific set of conditions. A reaction that occurs under the given set of conditions without any external driving force is called a spontaneous reaction. Otherwise, it is said to be non-spontaneous. In our day today life, we observe many spontaneous physical and chemical processes, which includes the following examples.

i.           A waterfall runs downhill, but never uphill, spontaneously.

ii.               A lump of sugar dissolves spontaneously in a cup of coffee, but never reappears in its original form spontaneously.

iii.               Heat flows from hotter object to a colder one, but never flows from colder to hotter object spontaneously.

iv.               The expansion of a gas into an evacuated bulb is a spontaneous process, the reverse process that is gathering of all molecules into one bulb is not. Spontaneous

These examples show that the processes that occur spontaneously in one direction, cannot take place in opposite direction spontaneously.

Similarly a large number of exothermic reactions are spontaneous. An example is combustion of methane.

CH₄+2O₂ → CO₂ + 2 H₂O

 ΔH^o = −890.4 kJ mol⁻¹

Another example is acid-base neutralization reaction:

H⁺ + OH⁻ → H₂O

ΔH^o= −57.32 kJ mol⁻¹

However, some endothermic processes are also spontaneous. For example ammonium nitrate dissolves in water spontaneously though this dissolution is endothermic.

NH₄NO₃  --^H2O→ NH⁺₄ + NO⁻₃

ΔH^o= + 25 kJ mol⁻¹

From the above examples we can come to the conclusion that exothermicity favors the spontaneity but does not guarantee it. We cannot decide whether or not a chemical reaction will occur spontaneously solely on the basis of energy changes in the system. We know from second law of thermodynamics that in a spontaneous process, the entropy increases. But not all the processes which are accompanied by an increase in entropy are spontaneous. In order to predict the spontaneity of a reaction, we need some other thermodynamic function.

The second law of thermodynamics introduces another thermodynamic function called Gibbs free energy which finds useful in predicting the spontaneity of a reaction. The Gibbs free energy (G) was developed in the 1870’s by Josiah Willard Gibbs. He originally termed this energy as the “available energy” to do work in a system. This quantity is the energy associated with a chemical reaction that can be used to do work.

Gibbs free energy is defined as below

G = H - TS ------------ (7.35)

Gibbs free energy (G) is an extensive property and it is a single valued state function.

Let us consider a system which undergoes a change of state from state (1) to state (2) at constant temperature.

G₂ – G₁ = (H₂ – H₁) – T(S₂ – S₁)

ΔG =ΔH – T ΔS−−−−−−(7.36)

Now let us consider how ΔG is related to reaction spontaneity.

We know that

ΔS_total = ΔS_sys + ΔS_surr

For a reversible process (equilibrium), the change in entropy of universe is zero. ΔS_total = 0 [∴ΔS_sys = −ΔS_surr]

Similarly, for an equilibrium process ΔG=0

For spontaneous process, ΔS_total > 0 , so

TΔS_sys − ΔH_sys<0

−(ΔH_sys− TΔS_sys)>0

−(ΔG ) > 0

hence for a spontaneous process,

ΔG < 0

i.e. ΔH – T ΔS < 0 −−−−−−(7.37)

ΔH_sys is the enthalpy change of a reaction, TΔS_sys is the energy which is not available to do useful work. So ΔG is the net energy available to do useful work and is thus a measure of the ‘free energy’. For this reason, it is also known as the free energy of the reaction. For non spontaneous process, ΔG > 0

Gibbs free energy and the net work done by the system:

For any system at constant pressure and temperature

ΔG = ΔH – T ΔS −−−− (7.36)

We know that,

ΔH =ΔU + PΔV

ΔG = ΔU + PΔV – TΔS from first law of thermodynamics

ΔU = q + w

from second law of thermodynamics

ΔG = w + PΔV

−ΔG = −w − PΔV ............(7.38)

But −PΔV represents the work done due to expansion against a constant external pressure. Therefore, it is clear that the decrease in free energy (–ΔG) accompanying a process taking place at constant temperature and pressure is equal to the maximum work obtainable from the system other than the work of expansion.

Criteria for spontaneity of a process

The spontaneity of any process depends on three different factors.

·           If the enthalpy change of a process is negative, then the process is exothermic and may be spontaneous. (ΔH is negative)

·           If the entropy change of a process is positive, then the process may occur spontaneously. (ΔS is positive)

·           The gibbs free energy which is the combination of the above two (ΔH -TΔS) should be negative for a reaction to occur spontaneously, i.e. the necessary condition for a reaction to be spontaneous is ΔH -TΔS < 0

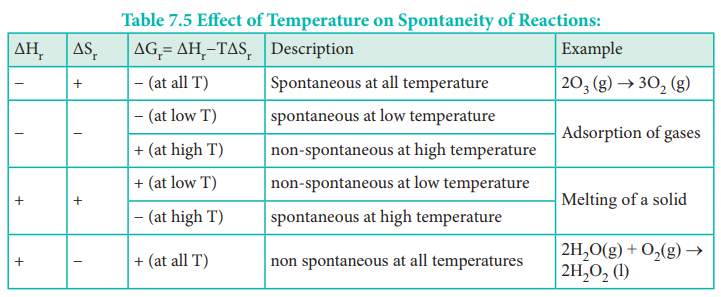
The Table assumes ΔH and ΔS will remain the way indicated for all temperatures. It may not be necessary that way. The Spontaneity of a chemical reaction is only the potential for the reaction to proceed as written. The rate of such processes is determined by kinetic factors, outside of thermodynamical prediction.

Problem: 7. 8

Relationship between standard free energy change (ΔG⁰) and equilibrium constant (K_eq):

In a reversible process, the system is in perfect equilibrium with its surroundings at all times. A reversible chemical reaction can proceed in either direction simultaneously, so that a dynamic equilibrium is set up. This means that the reactions in both the directions should proceed with decrease in free energy, which is impossible. It is possible only if at equilibrium, the free energy of a system is minimum. Lets consider a general equilibrium reaction

A+B ⇌  C + D

The free energy change of the above reaction in any state (ΔG) is related to the standard free energy change of the reaction (ΔG⁰ ) according to the following equation.

ΔG= ΔG⁰ + RT ln Q −−−−−−(7.39)

where Q is reaction quotient and is defined as the ratio of concentration of the products to the concentrations of the reactants under non equilibrium condition.

When equilibrium is attained, there is no further free energy change i.e. ΔG 0 and Q becomes equal to equilibrium constant. Hence the above equation becomes.

ΔG⁰ = –RT ln K_eq

This equation is known as Van’t Hoff equation.

ΔG⁰ = –2.303 RT log K_eq ----------(7.40)

We also know that

ΔG⁰ = ΔH⁰ – T ΔS⁰ = − RT ln K_eq

Problem: 7.9

Calculate ΔG⁰  for conversion of oxygen to ozone 3/2 O₂ ↔ O_3(g) at 298 K, if K_p for this conversion is 2.47 u 10⁻²⁹ in standard pressure units.

Solution:

ΔG⁰ = − 2.303 RT log K_p

Where

R = 8.314 JK⁻¹mol⁻¹

K_p = 2.47 x10⁻²⁹