Lattice energy

Lattice energy (∆H_lattice)

Lattice energy is defined as the amount of energy required to completely remove the constituent ions from its crystal lattice to an infinite distance. It is also referred as lattice enthalpy.

NaCl(s)  â†’ Na⁺(g) + Cl^–(g)

∆H_lattice = + 788 kJ mol^-1

From the above equation it is clear that 788 kJ of energy is required to separate Na⁺ and Cl^- ions from 1 mole of NaCl.

Born - Haber cycle

The Born–Haber cycle is an approach to analyse reaction energies. It was named after two German scientists Max Born and Fritz Haber who developed this cycle. The cycle is concerned with the formation of an ionic compound from the reaction of a metal with a halogen or other non-metallic element such as oxygen.

Born–Haber cycle is primarily used in calculating lattice energy, which cannot be measured directly. The Born–Haber cycle applies Hess's law to calculate the lattice enthalpy. For example consider the formation of a simple ionic solid such as an alkali metal halide MX, the following steps are considered.

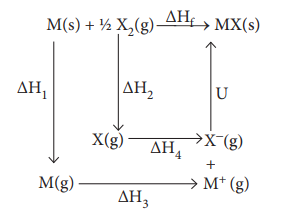
∆H₁ - enthalpy change for the sublimation M(s) to M(g)

ΔH₂- enthalpy change for the dissociation of ½ X₂ (g) to X(g)

∆H₃- Ionisation energy for M(g) to M⁺(g) ∆H₄ - electron affinity for the conversion of X(g) to X^-(g)

U - the lattice enthalpy for the formation of solid MX

∆H_f - enthalpy change for the formation of solid MX directly form elements According to Hess's law of heat summation

∆H_f  =  ∆H₁  +  ∆H ₂ +  ∆H ₃ +  ∆H ₄ + U

Let us use the Born - Haber cycle for determining the lattice enthalpy of NaCl as follows:

Since the reaction is carried out with reactants in elemental forms and products in their standard states, at 1 bar, the overall enthalpy change of the reaction is also the enthalpy of formation for NaCl. Also, the formation of NaCl can be considered in 5 steps. The sum of the enthalpy changes of these steps is equal to the enthalpy change for the overall reaction from which the lattice enthalpy of NaCl is calculated.

Let us calculate the lattice energy of sodium chloride using Born-Haber cycle

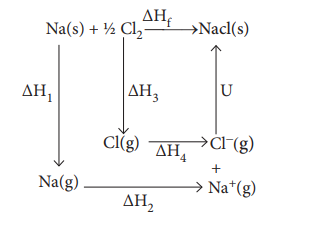
ΔH_f = heat of formation of sodium chloride = – 411.3 kJ mol^–1

ΔH₁ = heat of sublimation of Na(S) = 108.7 kJ mol^–1

ΔH₂ = ionisation energy of Na(S) = 495.0 kJ mol^–1

ΔH₃ = dissociation energy of Cl₂(S) = 244 kJ mol^–1

ΔH₄ = Electron affinity of Cl(S)= – 349.0 kJ mol^–1

U = lattice energy of NaCl

∆H_f = ∆H₁ + ∆H₂ + 1/2∆H₃ + ∆H₄ +U

U = (–411.3) – (108.7 + 495.0 + 122 – 349)

U = (–411.3) – (376.7)

U = – 788 kJ mol^–1

This negative sign in lattice energy indicates that the energy is released when sodium is formed from its constituent gaseous ions Na⁺ and Cl^-