Chapter: 11th Chemistry : UNIT 7 : Thermodynamics
Thermochemical Equations
Thermochemical
Equations:
A thermochemical equation is a balanced stoichiometric
chemical equation that includes the enthalpy change (ΔH). The following
conventions are adopted in thermochemical equations:
i.
The coefficients in a balanced thermochemical equation
refer to number of moles of reactants and products involved in the reaction.
ii.
The enthalpy change of the reaction ΔHr has to
be specified with appropriate sign and unit.
iii.
When the chemical reaction is reversed, the value of ΔH is
reversed in sign with the same magnitude.
iv.
The physical states (gas, liquid, aqueous, solid in
brackets) of all species are important and must be specified in a
thermochemical reaction, since ΔH depends on the physical state of reactants
and products.
v.
If the thermochemical equation is multiplied throughout by
a number, the enthalpy change is also multiplied by the same number.
vi.
The negative sign of ΔHr indicates that the
reaction is exothermic and the positive sign of ΔHr indicates an
endothermic reaction.
For example, consider the following reaction,
2 H2(g)+O2(g)ŌåÆ2 H2O(g) ╬öHr0 =ŌłÆ 967.4
kJ
2 H2 O (g) ŌåÆ2 H2(g) + O2(g) ╬öHr0 = + 967.4 kJ
Standard enthalpy of reaction (ΔHr0) from standard enthalpy of formation (ΔHf0 )
The standard enthalpy of a reaction is the enthalpy change
for a reaction when all the reactants and products are present in their
standard states. Standard conditions are denoted by adding the superscript 0 to
the symbol (ΔH0)
We can calculate the enthalpy of a reaction under standard
conditions from the values of standard enthalpies of formation of various
reactants and products. The standard enthalpy of reaction is equal to the
difference between standard enthalpy of formation of products and the standard
enthalpies of formation of reactants.
╬öHr0 = ╬Ż ╬öHr0 (products)
- ╬Ż ╬öHr0 (reactants)
For a general reaction
aA + bB ŌåÆ cC +dD
╬öHr0 = ╬Ż ╬öHr0
(products) - ╬Ż ╬öHr0 (reactants)
ΔHr0 = {c ΔHf0 (C)
+ d ΔHf0 (D)} -{a ΔHf0(A) + b ΔHf0(B)}
Problem : 7.2
The standard enthalpies of formation of C2H5OH(l),
CO2(g) and H2O(l) are - 277, -393.5 and -285.5 kJ mol-1
respectively.
Calculate the standard enthalpy change for the reaction
C2H5OH(l)+3O2(g) ŌåÆ2CO2(g)+ 3 H2O(l)
The enthalpy of formation of O2(g) in the
standard state is Zero, by definition
Solution:
For example, the standard enthalpy change for the
combustion of ethanol can be calculated from the standard enthalpies of
formation of C2H5OH(l), CO2(g) and H2O(l).
The enthalpies of formation are ŌĆō277, ŌĆō 393.5 and ŌĆō285.5 kJ molŌĆō1
respectively.
C3H5OH(l) + 3O2(g) ŌåÆ 2CO2(g) + 3H2O(l)

=[ ŌłÆ787 ŌłÆ 856 . 5] ŌłÆ [ ŌłÆ277]
= - 1643 .5 + 277
ŌłåH0r = ŌłÆ1366 . 5 KJ
Heat of combustion
The heat of combustion of a substance is defined as ŌĆ£The
change in enthalpy of a system when one mole of the substance is completely
burnt in excess of air or oxygenŌĆØ. It is denoted by ŌłåHC. For example, the heat of combustion of methane is ŌĆō
87.78 kJ mol-1
CH4(g)+ 2O2(g)ŌåÆ CO2(g)+
2H2O(l)
ŌłåHC = ŌĆō 87.78 kJ mol-1
For the combustion of carbon,
C (s)+ O2(g) ŌåÆ CO2(g)
ŌłåHC = ŌĆō 394.55 kJ mol-1
Combustion reactions are always exothermic. Hence the
enthalpy change is always negative.
Molar heat capacities
When heat (q) is supplied to a system, the molecules in
the system absorb the heat and hence their kinetic energy increases, which in
turn raises the temperature of the system from T1 to T 2.
This increase (T2 - T1) in temperature is directly
proportional to the amount of heat absorbed and the mass of the substance. In
other words,
q α mΔT
q = c mΔT
c = q/m ΔT
The constant c is called heat capacity.
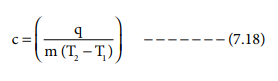
when m=1 kg and (T2 - T1) = 1 K then
the heat capacity is referred as specific heat capacity. The equation 7.18
becomes
c = q
Thus specific heat capacity of a system is defined as ŌĆ£The
heat absorbed by one kilogram of a substance to raise its temperature by one
Kelvin at a specified temperatureŌĆØ.
The heat capacity for 1 mole of substance, is called molar
heat capacity (cm). It is
defined as ŌĆ£The amount of heat absorbed by one mole of the substance to raise
its temperature by 1 kelvinŌĆØ.
Units of Heat Capacity:
The SI unit of molar heat capacity is JKŌłÆ1mol-1
The molar heat capacities can be expressed either at
constant volume (Cv) or at constant pressure (Cp).
According to the first law of thermodynamics
U = q + w or U = q - PdV
q = U + PdV ---------------------(7.19)
Differentiate (7.19) with respect to temperature at
constant volume i.e dV=0,
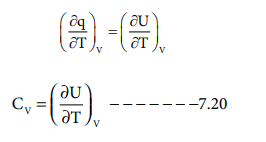
Thus the heat capacity at constant volume (CV)
is defined as the rate of change of internal energy with respect to temperature
at constant volume.
Similarly the molar heat capacity at constant pressure (CP)
can be defined as the rate of change of enthalpy with respect to temperature at
constant pressure.

Relation between Cp and Cv for an ideal gas.
From the definition of enthalpy
H=U+PV ------ (7.8)
for 1 mole of an ideal gas
PV = nRT ----- (7.22)
By substituting (7.22) in (7.8)
H = U + nRT ---- (7.23)
Differentiating the above equation with respect to T,
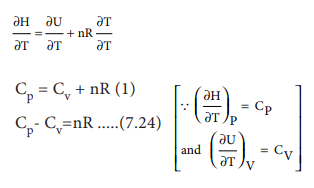
At constant
pressure processes, a system has to do work against the surroundings. Hence,
the system would require more heat to effect a given temperature rise than at
constant volume, so Cp is always greater than Cv
Calculation of ΔU and ΔH
For one mole of an ideal gas, we have
CV = dU / dT
dU = CV dT
For a finite change, we have
ŌłåU = CV ╬öT
ŌłåU= CV (T2 ŌĆō T1)
and for n moles of an ideal gas we get
╬öU = n Cv(T2 ŌĆō T1)
ŌĆōŌĆōŌĆōŌĆōŌĆōŌĆōŌĆōŌĆōŌĆōŌĆō (7.25)
Similarly for n
moles of an ideal gas we get
ŌłåH= n CP (T2-T1)ŌĆōŌĆōŌĆōŌĆōŌĆōŌĆō
(7.26)
Problem 7.3
Calculate the value of ŌłåU and ŌłåH on heating 128.0 g of
oxygen from 0o C to 1000 C. CV and CP
on an average are 21 and 29 J mol-1 K-1. (The difference
is 8Jmol-1 K-1 which is approximately equal to R)
Solution.
We know
ŌłåU = n Cv
(T2-T1)
ŌłåH = n CP
(T2- T1)
Here
n= 128/32 4 moles ;
T2 = 1000
C =373K;
T1 = 00
C = 273K
ŌłåU = n Cv
(T2-T1)
ŌłåU = 4
x 21 x (373 - 273)
ŌłåU = 8400
J
ŌłåU = 8.4
kJ
ŌłåH = n Cp (T2- T1)
ŌłåH = 4
├Ś 29 ├Ś (373- 273)
ŌłåH = 11600
J
ŌłåH = 11.6
kJ
Related Topics