Chapter: 11th Chemistry : UNIT 7 : Thermodynamics
Measurement of ΔU and ΔH using Calorimetry
Measurement
of ΔU and ΔH using Calorimetry.
Calorimeter is used for measuring the amount of heat
change in a chemical or physical change. In calorimetry, the temperature change
in the process is measured which is directly proportional to the heat capacity.
By using the expression C = q/mΔT, we can calculate the amount of heat change
in the process. Calorimetric measurements are made under two different
conditions
i.
At constant volume (qV)
ii.
At constant pressure (qp)
(A) ∆U Measurements
For chemical reactions, heat evolved at constant volume,
is measured in a bomb calorimeter.
The inner vessel (the bomb) and its cover are made of
strong steel. The cover is fitted tightly to the vessel by means of metal lid
and screws.
A weighed amount of the substance is taken in a platinum
cup connected with electrical wires for striking an arc instantly to kindle
combustion. The bomb is then tightly closed and pressurized with excess oxygen.
The bomb is immersed in water, in the inner volume of the calorimeter. A
stirrer is placed in the space between the wall of the calorimeter and the
bomb, so that water can be stirred, uniformly. The reaction is started by
striking the substance through electrical heating.
A known amount of combustible substance is burnt in oxygen
in the bomb. Heat evolved during the reaction is absorbed by the calorimeter as
well as the water in which the bomb is immersed. The change in temperature is
measured using a Beckman thermometer. Since the bomb is sealed its volume does
not change and hence the heat measurements is equal to the heat of combustion
at a constant volume (ΔU)c.
The amount of heat produced in the reaction (ΔU)c
is equal to the sum of the heat abosrbed by the calorimeter and water.
Heat absorbed by the calorimeter
q1 = k.ΔT
where k is a calorimeter constant equal to mc Cc
( mc is mass of the calorimeter and Cc is heat capacity
of calorimeter)
Heat absorbed by the water
q2 = mw Cw ΔT
where mw is molar mass of water
Cw is molar heat capacity of water
(4,184 kJ K-1 mol-1)
Therefore ΔUc = q1 + q2
=k.ΔT + mw Cw ΔT
=(k+mw Cw)ΔT
Calorimeter constant can be determined by burning a known
mass of standard sample (benzoic acid) for which the heat of combustion is
known (-3227 kJmol-1)
The enthalpy of combustion at constant pressure of the
substance is calculated from the equation (7.17)
ΔHC°(pressure) = ΔUC(Vol)
+ ΔngRT
Applications of bomb calorimeter:
1. Bomb calorimeter is used to determine the amount of
heat released in combustion reaction.
2. It is used to determine the calorific value of food.
3. Bomb calorimeter is used in many industries such as
metabolic study, food processing, explosive testing etc.
(b) ΔH Measurements
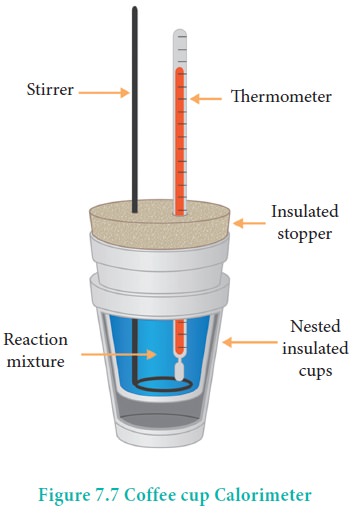
Heat change at constant pressure (at atmospheric pressure)
can be measured using a coffee cup calorimeter. A schematic representation of a
coffee cup calorimeter is given in Figure 7.7. Instead of bomb, a styrofoam cup
is used in this calorimeter. It acts as good adiabatic wall and doesn't allow
transfer of heat produced during the reaction to its surrounding. This entire
heat energy is absorbed by the water inside the cup. This method can be used
for the reactions where there is no appreciable change in volume. The change in
the temperature of water is measured and used to calculate the amount of heat
that has been absorbed or evolved in the reaction using the following
expression.
q = mw Cw ΔT
where mw is the molar mass of water and Cw
is the molar heat capacity of water (4184 kJ K-1 mol-1)
Problem 7. 4
Calculate the enthalpy of combustion of ethylene at 300 K
at constant pressure, if its heat of combustion at constant volume (ΔU) is
−1406 kJ .
The complete ethylene combustion reaction can be written
as,
C2H4 (g) + 3O2(g) → 2CO2
(g)+2H2O(l)
ΔU = −1406 kJ
∆n = np(g) - nr(g)
∆n = 2 - 4 = -2
∆H = ∆U + RTDng
∆H = -1406 + (8.314 × 10-3 × 300 ×(-2)
∆H = -1410.9 kJ
Applications of the heat of combustion:
1. Calculation of heat of formation:
Since the heat of combustion of organic compounds can be determined with considerable
ease, they are employed to calculate the heat of formation of other compounds.
For example let us calculate the 0 standard enthalpy of formation ΔHf of CH4 from the values of enthalpy of combustion for H2, C(graphite) and CH4 which are - 285.8, 393.5, and -890.4 kJ mol-1 respectively.
Let us interpret the information about enthalpy of
formation by writing out the equations. It is important to note that the
standard enthalpy of formation of pure elemental gases and elements is assumed
to be zero under standard conditions. Thermochemical equation for the formation
of methane from its constituent elements is,
C(graphite) + 2H2(g) → CH4(g)
ΔHf0
= X kJ mol-1--- (i)
Thermo chemical equations for the combustion of given
substances are,
H (g ) + 1/2 → H2O(
l)
ΔH0 = –285.8 kJ mol-1---(ii)
C(graphite) + O2→ CO2
ΔH0 = –393.5 kJ mol-1--- (iii)
CH4 (g) + 2 O2→CO2 (g)+
2H2O (l)
ΔH0 = –890.4 kJ mol-1--- (iv)
Since methane is in the product side of the required
equation (i), we have to reverse the equation (iv)
CO2 (g)+2 H2O (l) → CH4
(g) + 2 O2
ΔH0 = + 890.4 kJ mol-1--- (v)
In order to get equation (i) from the remaining,
(i) = [(ii) … 2] + (iii) + (v)
X = [(–285.8) … 2] + [–393.5] + [+ 890.4]
= –74.7 kJ
Hence, the amount of energy required for the formation of
1 mole of methane is -74.7 kJ
The heat of formation methane = -74.7 kJ mol-1
(2) Calculation of calorific value of food and fuels:
The calorific value is defined as the amount of
heat produced in calories (or joules) when one gram of the substance is
completely burnt. The SI unit of calorific value is J kg−1. However,
it is usually expressed in cal g-1.
Heat of solution:
Heat changes are usually observed when a substance is
dissolved in a solvent. The heat of solution is defined as the change in
enthalpy when one mole of a substance is dissolved in a specified quantity of
solvent at a given temperature.
Heat of neutralisation:
The heat of neutralisation is defined as “The change in
enthalpy when one gram equivalent of an acid is completely neutralised by one
gram equivalent of a base or vice versa in dilute solution”.
HCl(aq)+NaOH(aq) → NaCl (aq)+ H2O(l)
∆H = – 57.32 kJ
H+(aq) + OH-(aq) → H2O(l)
∆H = – 57.32 kJ
The heat of neutralisation of a strong acid and strong
base is around – 57.32 kJ, irrespective of nature of acid or base used which is
evident from the below mentioned examples.
HCl (aq) + KOH(aq) →KCl (aq) + H2O(l)
∆H = – 57.32 kJ
HNO3(aq)+KOH(aq)→KNO3(aq)+ H2O(l)
∆H = – 57.32 kJ
H2SO4(aq) + 2KOH(aq) → K2SO4(aq) +
2 H2O(l)
∆H = – 57.32 kJ
The reason for this can be explained on the basis of
Arrhenius theory of acids and bases which states that strong acids and strong
bases completely ionise in aqueous solution to produce H+ and OH-ions
respectively. Therefore in all the above mentioned reactions the neutralisation
can be expressed as follows.
H+(aq) + OH-(aq) → H2O(l)
∆H = – 57.32 kJ
Molar heat of fusion
The molar heat of fusion is defined as “the change in
enthalpy when one mole of a solid substance is converted into the liquid state
at its melting point”.
For example, the heat of fusion of ice can be represented
as
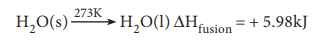
Molar heat of vapourisation
The molar heat of vaporisation is defined as “the change
in enthalpy when one mole of liquid is converted into vapour state at its
boiling point”.
For example, heat of vaporisation of water can be represented
as
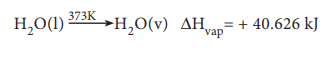
Molar heat of sublimation
Sublimation is a process when a solid changes directly
into its vapour state without changing into liquid state. Molar heat of
sublimation is defined as “the change in enthalpy when one mole of a solid is
directly converted into the vapour state at its sublimation temperature”. For
example, the heat of sublimation of iodine is represented as
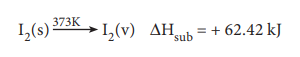
Another example of sublimation process is solid CO2
to gas at atmospheric pressure at very low temperatures.
Heat of transition
The heat of transition is defined as “The change in
enthalpy when one mole of an element changes from one of its allotropic form to
another. For example, the transition of diamond into graphite may be
represented as
C(diamond) → C
(graphite)
∆Htrans= +13.81 kJ
Similarly the allotropic transitions in sulphur and
phsphorous can be represented as follows,
S(monoclinic) →S(rhombic)
∆Htrans= – 0.067 kJ
P(white) → P(red)
∆Htrans = – 4.301 kJ
Related Topics