Explanation, Example Solved Problems | Algebra | Maths - Value and Zeros of a Polynomial | 9th Maths : UNIT 3 : Algebra
Chapter: 9th Maths : UNIT 3 : Algebra
Value and Zeros of a Polynomial
Value and Zeros of a Polynomial
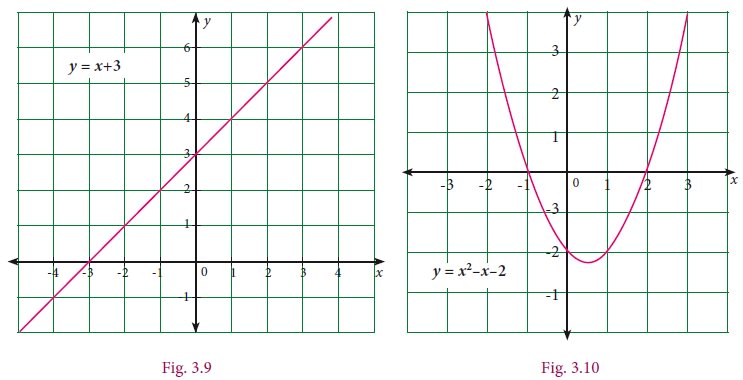
Consider the two graphs given below. The first is linear, the second is quadratic. The first intersects the X axis at one point (x = –3) and the second at two points (x = -1 and x = 2) . They both intersect the Y axis only at one point. In general, every polynomial has a graph and the graph is shown as a picture (since we all like pictures more than formulas, don’t we?). But also, the graph contains a lot of useful information – like whether it is a straight line, what is the shape of the curve, how many places it cuts the x-axis, etc.
How do you plot the graph of the polynomial ? You already know the answer. Put in different values of x and you get different values for the polynomial. If we put x=5 and calculate, we get the value of the polynomial at x=5. In general, the value of a polynomial p(x) at x=a, denoted p(a), is obtained by replacing x by a, where a is any real number.
Notice that the value of p(x) can be zero for many possible values of x (as in the second graph below). So it is interesting to ask, for how many values of x, does p(x) become zero, and for which values ? We call these values of x, the Zeros of the polynomial p(x).
Once we see that the values of the polynomial are what we plot in the graph of the polynomial, it is also easy to notice that the polynomial becomes zero exactly when the plot intersects the X-axis.
Can a polynomial p(x) have no zeros at all ? Now you have to think like a mathematician. If a polynomial has degree 1, it is going to be of the form ax+b, and you can solve ax+b = 0 to see that it will have some value of x that solves the equation. So it has one zero. What is the polynomial that has degree zero ? That means it has only a constant, some number r. But if r is non-zero, then it can never have value zero ! So yes, the constant polynomial can have no zeroes at all.
Can we argue that every polynomial p(x) with positive degree has a zero ? That is the same as saying that every polynomial p(x) = 0 has a solution ! But this is not true, since x2 +1 = 0 has no solution in the set of real numbers. The polynomial x2+1 has only positive values, never intersects the X-axis.
So we see that a polynomial may or may not have zeros and may have one or more zeroes. So it is very interesting, given any polynomial, to figure out whether it has zeros or not, and how many it can have.
Can a polynomial have infinitely many zeros ?
That is, it is a special polynomial that keeps intersecting the X-axis again and again and again and …. at newer and newer values of x. Now, there is a theorem that assures us that a polynomial of degree has atmost many zeros. (We will have to learn a good deal of Mathematics before we can prove that theorem, but when you learn you will see that it is beautiful and worth the wait !)
We will now state all this in formal definitions.
(The number of zeros depends on the line or curves intersecting x axis.)
For Fig. 3.9, Number of zeros is equal to 1
For Fig. 3.10, Number of zeros is equal to 2

1. Value of a Polynomial
Value of a polynomial p(x) at x = a is p (a) obtained on replacing x by a (a∈R)
For example,
Consider f(x) = x3+3x-1.
The value of f(x) at x = 2 is
f(2) = 22+3(2)-1=4+6-1=9.
2. Zeros of Polynomial
(i) Consider the polynomial p(x) = 4x3 -6x2+ 3x –14
The value of p(x) at x = 1 is
p(1) = 4(1)3 – 6(1)2 + 3(1) – 14
= 4 – 6 + 3 – 14
= –13
Then, we say that the value of p(x) at x = 1 is – 11.
If we replace x by 0, we get
p(0) = 4(0)3 – 6(0)2 + 3(0) –14
= 0 – 0 + 0 – 14
= –14
we say that the value of p(x) at x = 0 is – 14.
The value of p(x) at x = 2 is p(2) = 4(2)3 – 6(2)2 + 3(2) – 14
= 32 – 24 + 6 – 14
= 0
Since the value of p(x) at x = 0 is zero, we can say that 2 is one of the zeros of p(x) where p(x) = 4x3 –6x2 + 3x –14.
3. Roots of a Polynomial Equation
In general, if p(a) = 0 we say that a is zero of polynomial p(x) or a is the root of polynomial equation p(x) = 0
Example 3.7
If f(x) = x2-4x+3, find the values of f(1),f(-1),f(2),f(3). Also find the zeros of the polynomial f(x).
Solution
f(x)=x2-4x+3
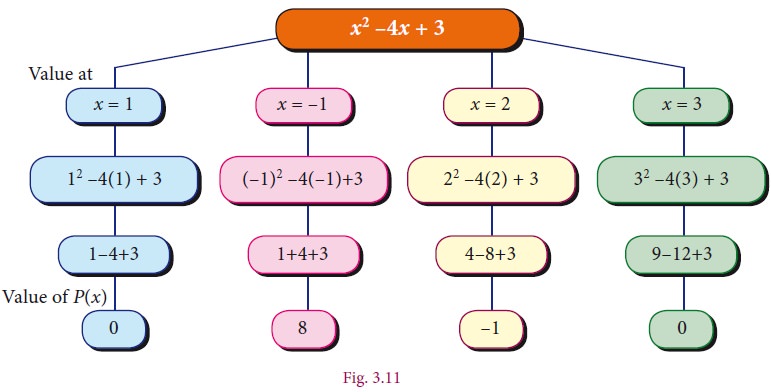
Since the value of the polynomial f(x) at x = 1 and x = 3 is zero, as the zeros of polynomial
f(x) are 1 and 3.
Example 3.8
Find the Zeros of the following polynomials.
(i) f(x) = 2x + 1 (ii) f(x) = 3x – 5
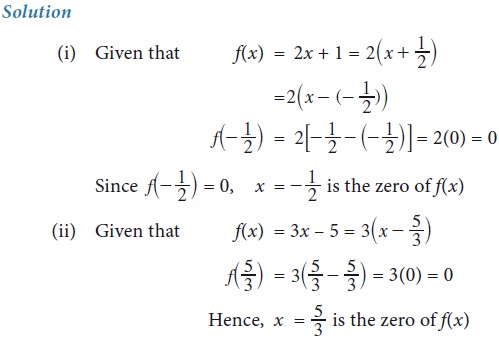
Example 3.9
Find the roots of the following polynomial equations.
(i) 5x – 3 = 0 (ii) –7 –4x = 0

Example 3.10
Check whether –3 and 3 are zeros of the polynomial x2 – 9
Solution
Let f(x) = x2 – 9
Then, f(–3) = (–3)2 – 9 = 9 – 9 = 0
f(+3) = 32 – 9 = 9 – 9 = 0
-3 and 3 are zeros of the polynomial x2 – 9
Related Topics