Exercise 3.1: Polynomials

Exercise 3.1

1. Which of the following expressions are polynomials. If not give reason:

(i) 1/x² + 3x − 4 (ii) x² (x − 1) (iii) 1/x (x + 5) (iv) 1/x^-2 + 1/x^-1 + 7 (v) √5 x² + √3 x + √2 (vi) m² − ³√m + 7m − 10

2. Write the coefficient of x² and x in each of the following polynomials.

(i) 4 + 2/5 x² − 3x (ii) 6 − 2x² + 3x³ − √7x (iii) πx² − x + 2 (iv) √3 x² + √2 x + 0.5 (v) x² – 7/2 x + 8

3. Find the degree of the following polynomials.

(i) 1 − √2 y² + y⁷ (ii) [ x³ − x⁴ + 6x⁶ ] / x² (iii) x³ ( x² + x) (iv) 3x⁴ + 9x² + 27x⁶ (v) 2√5 p⁴ − 8p³/√3 + 2p²/7

4. Rewrite the following polynomial in standard form.

(i) x − 9 + √7x³ + 6x² (ii) √2x² – 7/2 x⁴ + x − 5x³ (iii) 7x³ – 6/5 x² + 4x − 1 (iv) y² + √5y³ − 11 – 7/3y + 9y⁴

5. Add the following polynomials and find the degree of the resultant polynomial.

(i) p (x) = 6x² − 7x + 2 ; q(x) = 6x³ − 7x + 15

(ii) h (x) = 7x³ − 6x + 1 ; f(x) = 7x² + 17x − 9

(iii) f(x) = 16x⁴ − 5x² + 9 ;  g(x) = − 6x³ + 7x – 15

6. Subtract the second polynomial from the first polynomial and find the degree of the resultant polynomial.

(i) p(x) = 7x² + 6x – 1 ;  q ( x) = 6x – 9

(ii) f (y) = 6y² − 7y + 2 ; g ( y) = 7y + y³

(iii) h ( z) = z⁵ − 6z⁴ + z ; f ( z) = 6z² + 10z – 7

7. What should be added to 2x³ + 6x² − 5x + 8 to get 3x³ − 2x² + 6x + 15 ?

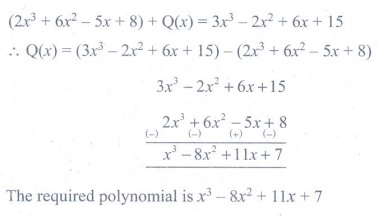
8. What must be subtracted from 2x⁴ + 4x² − 3x + 7 to get 3x³ − x² + 2x + 1 ?

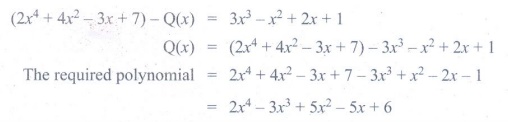
9. Multiply the following polynomials and find the degree of the resultant polynomial:

(i) p ( x) = x² – 9 ; q ( x) = 6x² + 7x – 2

(ii) f ( x) = 7x + 2 ; g (x ) = 15x – 9

(iii) h ( x) = 6x² − 7x + 1 ; f ( x) = 5x – 7

10. The cost of a chocolate is Rs. (x + y) and Amir bought (x + y) chocolates. Find the total amount paid by him in terms of x and y. If x =10, y =5 find the amount paid by him.

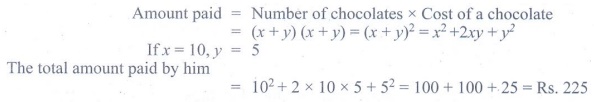
11. The length of a rectangle is (3x+2) units and it’s breadth is (3x–2) units. Find its area in terms of x. What will be the area if x = 20 units.

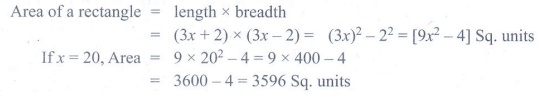
12. p (x) is a polynomial of degree 1 and q (x)  is a polynomial of degree 2. What kind of the polynomial p(x) × q(x) is ?