Solving by Elimination Method

Solving by Elimination Method

This is another algebraic method for solving a pair of linear equations. This method is more convenient than the substitution method. Here we eliminate (i.e. remove) one of the two variables in a pair of linear equations, so as to get a linear equation in one variable which can be solved easily.

The various steps involved in the technique are given below:

Step 1: Multiply one or both of the equations by a suitable number(s) so that either the coefficients of first variable or the coefficients of second variable in both the equations become numerically equal.

Step 2: Add both the equations or subtract one equation from the other, as obtained in step 1, so that the terms with equal numerical coefficients cancel mutually.

Step 3: Solve the resulting equation to find the value of one of the unknowns.

Step 4: Substitute this value in any of the two given equations and find the value of the other unknown.

Example 3.50

Given 4a + 3b = 65 and a + 2b = 35 solve by elimination method.

Solution

Thus the solution is a = 5, b = 15.

Example 3.51

Solve for x and y: 8x − 3y = 5xy, 6x − 5y = −2xy by the method of elimination.

Solution

The given system of equations are

8x − 3y = 5xy ...(1)

6x − 5y = −2xy ...(2)

Observe that the given system is not linear because of the occurrence of xy term. Also note that if x =0, then y =0 and vice versa. So, (0,0) is a solution for the system and any other solution would have both x ≠ 0 and y ≠ 0.

Let us take up the case where x ≠ 0, y ≠ 0.

Dividing both sides of each equation by xy,

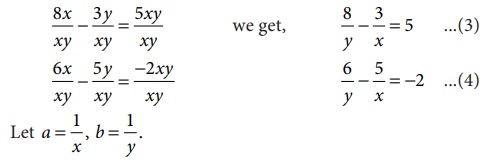
(3)&(4) respectively become, 8b − 3a = 5          ………..(5)

 6b − 5a = −2       ………..(5)

which are linear equations in a and b.

To eliminate a, we have,

 (5) × 5 ⇒ 40b − 15a = 25 .....(7)

 (6)×3⇒ 18b − 15a = −6 .....(8)

Now proceed as in the previous example to get the solution (11/23  22/31).

Thus, the system have two solutions (11/23  22/31) and ( 0, 0) .