Solving by Substitution Method

Solving by Substitution Method

In this method we substitute the value of one variable, by expressing it in terms of the other variable to reduce the given equation of two variables into equation of one variable (in order to solve the pair of linear equations). Since we are substituting the value of one variable in terms of the other variable, this method is called substitution method.

The procedure may be put shortly as follows:

Step 1: From any of the given two equations, find the value of one variable in terms of the other.

Step 2: Substitute the value of the variable, obtained in step 1 in the other equation and solve it.

Step 3: Substitute the value of the variable obtained in step 2 in the result of step 1 and get the value of the remaining unknown variable.

Example 3.48

Solve the system of linear equations x + 3y = 16 and 2x − y = 4 by substitution method.

Solution

Given x + 3y = 16 ... (1)

2x – y = 4 ... (2)

Example 3.49

The sum of the digits of a given two digit number is 5. If the digits are reversed, the new number is reduced by 27. Find the given number.

Solution

Let x be the digit at ten’s place and y be the digit at unit place.

Given that x + y = 5 …… (1)

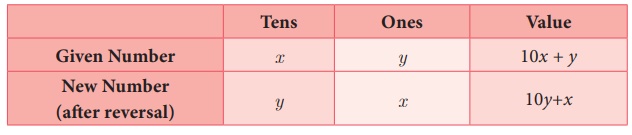
Given, Original number − reversing number = 27

(10x + y) – (10y + x) = 27

 10x − x + y − 10 y = 27

 9x − 9 y = 27

⇒ x − y = 3 ... (2)

Also from (1), y = 5 – x ... (3)

Substitute (3) in (2) to get x − (5 − x) = 3

 x − 5 + x = 3

2x = 8

x = 4

Substituting x = 4 in (3), we get y = 5 − x = 5 – 4

y = 1

Thus, 10x + y = 10 × 4 + 1 = 40 + 1 = 41.

Therefore, the given two-digit number is 41.