Simultaneous Linear Equations

Simultaneous Linear Equations

With sufficient background of graphing an equation, now we are set to study about system of equations, particularly pairs of simultaneous equations.

What are simultaneous linear equations? These consists of two or more linear equations with the same variables.

Why do we need them? A single equation like 2x+y =10 has an unlimited number of solutions. The points (1,8), (2,6), (3,4) and many more lie on the graph of the equation, which means these are some of its endless list of solutions. To be able to solve an equation like this, another equation needs to be used alongside it; then it is possible to find a single ordered pair that solves both equations at the same time.

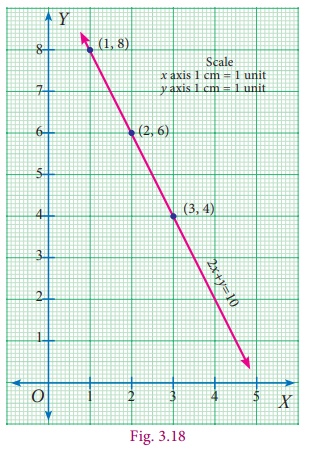
The equations we consider together in such settings make a meaningful situation and are known as simultaneous linear equations.

Real life Situation to understand the simultaneous linear equations

Consider the situation, Anitha bought two erasers and a pencil for ₹10. She does not know the individual cost of each. We shall form an equation by considering the cost of eraser as ‘x’ and that of pencil as ‘y’.

That is 2x + y = 10 ... (1)

Now, Anitha wants to know the individual cost of an eraser and a pencil. She tries to solve the first equation, assuming various values of x and y.

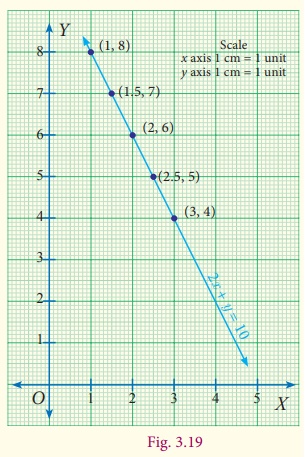
 2 × cost of eraser + 1 × cost of pencil = 10

2(1)+8 =10

2(1.5)+7 =10

2(2)+6 =10

2(2.5)+5 =10

2(3)+4 =10

:        :

:        :

Points to be plotted :

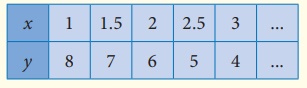
She gets infinite number of answers. So she tries to find the cost with the second equation.

Again, Anitha needs some more pencils and erasers. This time, she bought 3 erasers and 4 pencils and the shopkeeper received ₹30 as the total cost from her. We shall form an equation like the previous one.

The equation is 3x + 4y = 30 ...(2)

Even then she arrives at an infinite number of answers.

 3 × cost of eraser + 4 × cost of pencil = 30

3(2)+4 (6) = 30

3(4)+4 (4.5) = 30

3(6)+4 (3) = 30

3(8)+4 (1.5) = 30

         :                :

         :                :

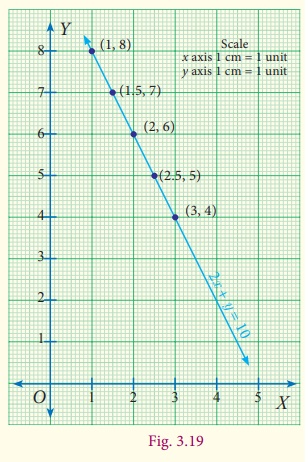
Points to be plotted :

While discussing this with her teacher, the teacher suggested that she can get a unique answer if she solves both the equations together.

By solving equations (1) and (2) we have the cost of an eraser as ₹2 and cost of a pencil as ₹6. It can be visualised in the graph.

The equations we consider together in such settings make a meaningful situation and are known as simultaneous linear equations.

Thus a system of linear equations consists of two or more linear equations with the same variables. Then such equations are called Simultaneous linear equations or System of linear equations or a Pair of linear equations.

Example 3.43

Check whether (5, −1) is a solution of the simultaneous equations x– 2y = 7 and 2x + 3y = 7.

Solution

Given x – 2y = 7 …(1)

2x + 3y = 7 …(2)

When x = 5, y = −1 we get

From (1) x – 2y = 5 – 2(−1) = 5 + 2 = 7 which is RHS of (1)

From (2) 2x + 3y = 2(5) + 3(−1) = 10−3 = 7 which is RHS of (2)

Thus the values x = 5, y = −1 satisfy both (1) and (2) simultaneously. Therefore (5,−1) is a solution of the given equations.

Progress Check

Examine if (3,3) will be a solution for the simultaneous linear equations 2x – 5y – 2 = 0 and x + y – 6 = 0 by drawing a graph.