Consistency and Inconsistency of Linear Equations in Two Variables

Consistency and Inconsistency of Linear Equations in Two Variables

Consider linear equations in two variables say

a₁ x + b₁ y + c₁ = 0 ...(1)

a₂ x + b₂ y + c₂ = 0 ...(2)

where a ₁ , a₂ , b₁ , b₂ , c₁ and c₂ are real numbers.

Then the system has :

Example 3.54

Check whether the following system of equation is consistent or inconsistent and say how many solutions we can have if it is consistent.

(i) 2x – 4y = 7; x – 3y = –2

(ii) 4x + y = 3 ; 8x + 2y = 6

(iii) 4x +7 = 2 y ; 2x + 9 = y

Solution

Example 3.55

Check the value of k for which the given system of equations kx + 2y = 3; 2x − 3y = 1 has a unique solution.

Solution

Given linear equations are

kx + 2 y = 3 .....(1) [a₁ x + b₁ y + c₁ = 0]

2x − 3y = 1 .....(2)   [a x + b y + c = 0 ]

Here a₁ = k, b₁ = 2, a₂ = 2, b₂ = −3 ;

For unique solution we take a₁/a₂ ≠ b₁/b₂ ; therefore k/2 ≠ 2/-3 ; k ≠ 4/-3 , that is k ≠ − 4/3 .

Example 3.56

Find the value of k, for the following system of equation has infinitely many solutions. 2x − 3y = 7; (k + 2)x − (2k + 1)y = 3(2k −1)

Solution

Given two linear equations are

 2x − 3y = 7  [a₁ x + b₁ y + c₁ = 0 ]

 (k + 2)x − (2k + 1)y = 3(2k − 1) [a₂x + b₂ y + c₂ = 0 ]

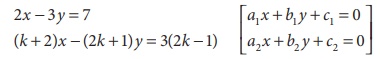
Here a₁ = 2, b₁ = −3, a₂ = (k + 2), b₂ = −(2k + 1), c₁ = 7, c₂ = 3(2k −1)

For infinite number of solution we consider

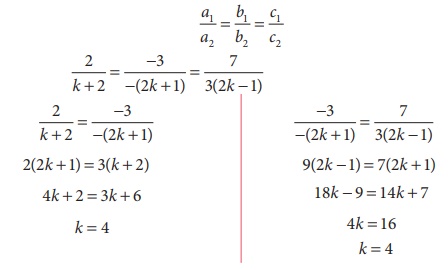
Example 3.57

Find the value of k for which the system of linear equations 8x + 5y = 9; kx + 10 y = 15 has no solution.

Solution Given linear equations are

8x + 5y = 9  [ a₁ x + b₁ y + c₁ = 0]

kx + 10 y = 15 [a₂ x + b₂ y + c₂ = 0]

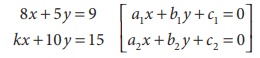
Here a₁ = 8, b₁ = 5, c₁ = 9, a₂ = k , b₂ = 10, c₂ = 15

For no solution, we know that

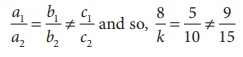
 a₁/a₂ = b₁/b₂ ≠ c₁/c₂ and so, 8/k = 5/10 ≠ 9/15

80 = 5k

k= 16

Activity – 3

1. Find the value of k for the given system of linear equations satisfying the condition below:

(i) 2x + ky = 1; 3x − 5y = 7 has a unique solution

(ii) kx + 3y = 3; 12x + ky = 6 has no solution

(iii) (k − 3)x + 3y = k; kx + ky = 12 has infinite number of solution

Solution:

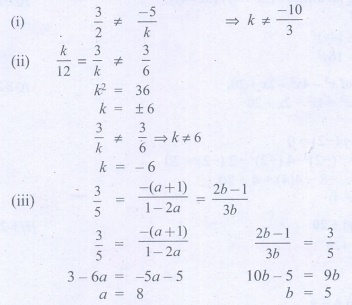
2. Find the value of a and b for which the given system of linear equation has infinite number of solutions 3x − (a + 1)y = 2b −1, 5x + (1 − 2a)y = 3b

Solution:

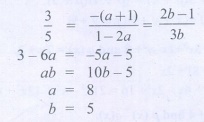
Activity – 4

For the given linear equations, find another linear equation satisfying each of the given condition

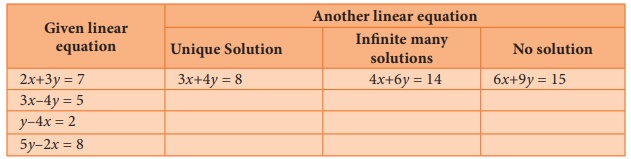
Solution: