Exercise 3.15: Multiple choice questions

Exercise 3.15

Multiple choice questions

1. If x³ + 6x² + kx + 6 is exactly divisible by (x + 2), then k= ?

(1) –6

(2) –7

(3) –8

(4) 11

Solution:

P(-2) = (-2)³ + 6(-2)² + k(-2) + 6 = 0

-8 + 24 – 2k +6  = 0

22 = 2k

k = 11

[Answer: (4) 11 ]

2. The root of the polynomial equation 2x + 3 = 0 is

(1) 1/3

(2) – 1/3

(3) – 3/2

(4) – 2/3

[Answer: (3) – 3/2 ]

3. The type of the polynomial 4–3x³ is

(1) constant polynomial

(2) linear polynomial

(3) quadratic polynomial

(4) cubic polynomial.

[Answer: (4) cubic polynomial ]

4. If x⁵¹ + 51 is divided by x + 1, then the remainder is

(1) 0

(2) 1

(3) 49

(4) 50

Solution: P (−1) = (−1)⁵¹ + 51 = −1 +51 =50

[Answer: (4) 50 ]

5. The zero of the polynomial 2x+5 is

(1) 5/2

(2) – 5/2

(3) 2/5

(4) – 2/5

[Answer: (2) – 5/2 ]

6. The sum of the polynomials p(x) = x³ – x² – 2, q(x) = x²–3x+ 1

(1) x³ – 3x – 1

(2) x³ + 2x² – 1

(3) x³ – 2x² – 3x

(4) x³ – 2x² + 3x –1

Solution: 

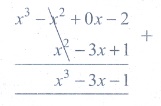
[Answer: (1) x³ – 3x – 1 ]

7. Degree of the polynomial (y³–2)(y³ + 1) is

(1) 9

(2) 2

(3) 3

(4) 6

Solution: (y³–2)(y³+1) = (y³–2)(y³–2) × 1 = y⁶ –2y³–2 = y⁶–y³–2

[Answer: (4) 6 ]

8. Let the polynomials be

(A) –13q⁵ + 4q² + 12q

(B) (x² +4 )(x² + 9)

(C) 4q⁸ – q⁶ + q²

(D) – 5/7 y¹² + y³ + y⁵

Then ascending order of their degree is

(1) A,B,D,C

(2) A,B,C,D

(3) B,C,D,A

(4) B,A,C,D

Solution: Degree of (A), (B) (C) & (D) are respectively be 5,4,8,12

[Answer: (4) B,A,C,D ]

9. If p(a ) = 0 then (x -a) is a ___________ of p(x)

(1) divisor

(2) quotient

(3) remainder

(4) factor

[Answer: (4) factor ]

10. Zeros of (2 − 3x) is ___________

(1) 3

(2) 2

(3) 2/3

(4) 3/2

Solution:

2−3x = 0

−3x = −2

x=2/3

[Answer: (3) 2/3 ]

11. Which of the following has x -1 as a factor?

(1) 2x -1

(2) 3x − 3

(3) 4x − 3

(4) 3x − 4

Solution:

P(x) = 3x−3

P(1) = 3(1)−3=0

So (x−1) is a factor of P(x)

[Answer: (2) 3x − 3 ]

12. If x − 3 is a factor of p(x), then the remainder is

(1) 3

(2) –3

(3) p(3)

(4) p(–3)

[Answer: (3) p(3) ]

13. (x + y )(x² −xy +y² ) is equal to

(1) (x + y)³

(2) (x -y)³

(3) x ³ + y³

(4) x ³ -y³

[Answer: (3) x ³ + y³ ]

14. (a + b −c)² is equal to __________

 (1) (a − b +c)²

(2) (−a −b +c)²

(3) (a + b +c)²

(4) (a − b -c)²

Solution:

(a+b−c)² = [−(−a−b+c)]² = (−a−b+c)²

[Answer: (2) (−a −b +c)² ]

15. If (x + 5) and (x − 3) are the factors of ax ² + bx +c, then values of a, b and c are

(1) 1,2,3

(2) 1,2,15

(3) 1,2, −15

(4) 1, −2,15

Solution:

P(−5) = a(−5²)+b(−5)+c = 25a−5b+c = 0 ….(1)

P(3) = a(3²)+bc + 3 + c = 9 + 3b + c = 0 ….(2)

25a−5b = 9a−3b

25a−9a = 3b+5b

16a=8b

a/b = 8/16 = 1/2

Substitute a=1, b=2 in (1)

25(1) – 5(2) = − c

25 – 10 = 15 = −c

C = −15

  [Answer: (3) 1,2, −15 ]

16. Cubic polynomial may have maximum of ___________ linear factors

(1) 1

(2) 2

(3) 3

(4) 4

[Answer: (3) 3 ]

17. Degree of the constant polynomial is __________

(1) 3

(2) 2

(3) 1

(4) 0

[Answer: (4) 0 ]

18. In an expression ax² + bx + c the sum and product of factors respectively,

(1) a,bc

(2) b,ac

(3) ac,b

(4) bc,a

[Answer: (2) b,ac ]

19. Find the value of m from the equation 2x + 3y = m . If its one solution is x = 2 and y = −2.

(1) 2

(2) −2

(3) 10

(4) 0

Solution:

x=2, y=−2

2x+3y=m,

m=2(2)+3(−2)

=4−6= −2

[Answer: (2) −2 ]

20. Which of the following is a linear equation

(1) x + 1/x = 2

(2) x ( x − 1) = 2

(3) 3x + 5 = 2/3

(4) x³ − x = 5

Solution:

x + [1/x] = 2

x²−2x+1=0

x(x−1) = 2

x²−x−2=0

[Answer: (3) 3x + 5 = 2/3 ]

21. Which of the following is a solution of the equation 2x − y = 6

(1) (2,4)

(2) (4,2)

(3) (3, −1)

(4) (0,6)

Solution:

2x−y=6

2(4) – 2 = 8−2=6=RHS

[Answer: (2) (4,2) ]

22. If (2,3) is a solution of linear equation 2x + 3y = k then, the value of k is

(1) 12

(2) 6

(3) 0

(4) 13

Solution:

2x+3y=k

2(2)+3(3)=4+9=13

[Answer: (4) 13 ]

23. Which condition does not satisfy the linear equation ax + by + c = 0

(1) a ≠ 0 , b = 0

(2) a = 0 , b ≠ 0

(3) a = 0 , b = 0 , c ≠ 0

(4) a ≠ 0 , b ≠ 0

Solution:

a=0, b=0, c≠0

(0)x + (0)y+c=0 False

[Answer: (3) a = 0 , b = 0 , c ≠ 0 ]

24. Which of the following is not a linear equation in two variable

(1) ax + by + c = 0

(2) 0x + 0 y + c = 0

(3) 0x + by + c = 0

(4) ax + 0 y + c = 0

Solution:

a and b both can not be zero

[Answer: (2) 0x + 0 y + c = 0 ]

25. The value of k for which the pair of linear equations 4x + 6 y −1 = 0 and 2x + ky − 7 = 0 represents parallel lines is

(1) k = 3

(2) k = 2

(3) k = 4

(4) k = −3

Solution:

4x+6y = 1

6y = −4x + 1

y = −4/6  x  + 1/6  ………. (1)

2x+ky−7=0

ky=−2x+7

 y = −2/k   x + 7/k  ………..(2)

Since the lines (1) and (2) parallel

m₁ = m₂

−4/6 = −2/k

k=3

[Answer: (1) k = 3 ]

26. A pair of linear equations has no solution then the graphical representation is

Solution:

Parallel lines have no solution

[Answer: (2) ]

27. If a₁/a₂ ≠ b₁/b₂ where a₁x + b₂y + c₁ = 0 and a₂x + b₂y + c₂ = 0 then the given pair of linear equation has __________ solution(s)

(1) no solution

(2) two solutions

(3) unique

(4) infinite

Solution:

a₁/a₂ ≠ b₁/b₂ ; unique solution

[Answer: (3) unique ]

28. If a₁/a₂ ≠ b₁/b₂ ≠ c₁/c₂ where a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0 then the given pair of linear equation has __________ solution(s)

(1) no solution

(2) two solutions

(3) infinite

(4) unique

Solution:

a₁/a₂ = b₁/b₂ ≠ c₁/c₂ :parallel

[Answer: (1) no solution ]

29. GCD of any two prime numbers is __________

(1) −1

(2) 0

(3) 1

(4) 2

[Answer: (3) 1 ]

30. The GCD of x ⁴ -y⁴ and x ² -y² is

(1) x ⁴ − y⁴

(2) x ² − y²

(3) (x + y)²

(4) (x + y)⁴

Solution:

x⁴−y⁴ = (x²)² – (y²)² = (x²+y²) (x²−y²)

x²−y²=x²−y²

G.C.D is = x² – y²

[Answer: (2) x ² -y² ]