Solving by Cross Multiplication Method

Solving by Cross Multiplication Method

The substitution and elimination methods involves many arithmetic operations, whereas the cross multiplication method utilize the coefficients effectively, which simplifies the procedure to get the solution. This method of cross multiplication is so called because we draw cross ways between the numbers in the denominators and cross multiply the coefficients along the arrows ahead. Now let us discuss this method as follows:

Suppose we are given a pair of linear simultaneous equations such as

a₁ x + b₁ y +c₁ = 0 ...(1)

a₂ x + b₂ y + c₂ = 0 ...(2)

such that a₁/a₂ ≠ b₁/b₂ . We can solve them as follows :

(1) × b₂ – (2) × b₁ gives b₂ (a₁ x + b₁ y +c₁ ) − b₁(a₂ x + b₂ y +c₂ ) = 0

 ⇒ x (a₁b₂ − a₂b₁ ) = (b₁c₂ − b₂c₁)

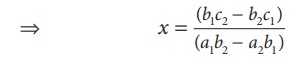
 (1) × a₂ – (2) × a₁ similarly can be considered and that will simplify to

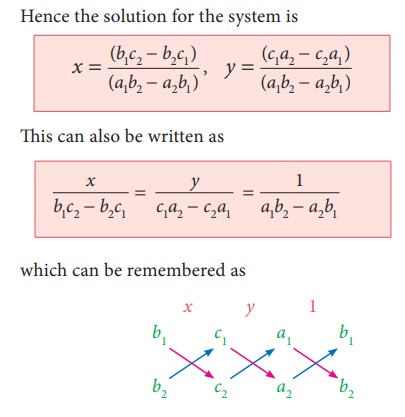
 y = (c₁a₂ − c₂a₁)  / (a₁b₂ – a₂b₂ )

 Hence the solution for the system is

Example 3.52

Solve 3x − 4 y = 10 and 4x + 3y = 5 by the method of cross multiplication.

Solution

The given system of equations are

3x − 4 y = 10 ⇒ 3x − 4 y −10 = 0 .....(1)

4x + 3y = 5 ⇒ 4x + 3y − 5 = 0 .....(2)

For the cross multiplication method, we write the co-efficients as

Thus the solution is x = 2, y = –1.

Example 3.53

Solve by cross multiplication method : 3x + 5y = 21; −7 x − 6 y = −49

Solution

The given system of equations are 3x + 5y − 21 = 0; −7 x − 6 y + 49 = 0

Now using the coefficients for cross multiplication, we get,

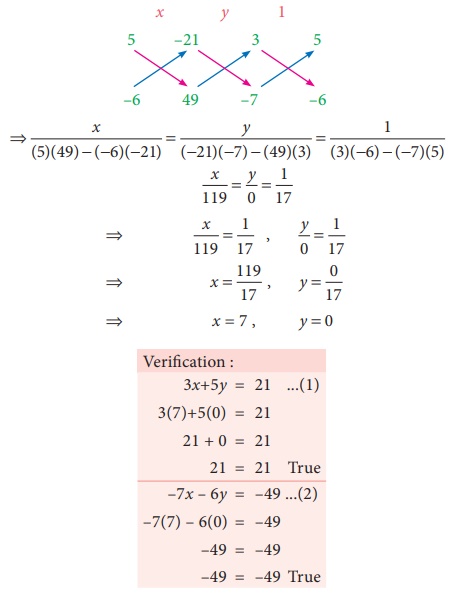
Note

Here y /0 = 1/17 is to mean y = 0/17 . Thus, y /0 is only a notation and it is not division by zero. It is always true that division by zero is not defined.