Factorisation

Factorisation

Factorisation is the reverse of multiplication.

For Example : Multiply 3 and 5; we get product 15.

Factorise 15; we get factors 3 and 5.

For Example : Multiply (x + 2) and (x + 3); we get product x ² + 5x + 6 .

Factorise x ² + 5x + 6 ; we get factors (x + 2) and (x + 3).

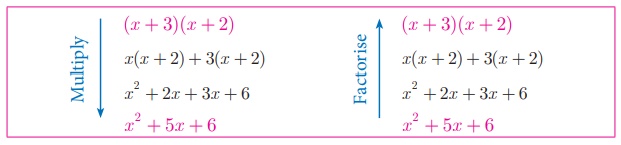
Thus, the process of converting the given higher degree polynomial as the product of factors of its lower degree, which cannot be further factorised is called factorisation.

Two important ways of factorisation are :

(i) By taking common factor

ab +ac

a × b + a × c

a (b +c) factored form

(ii) By grouping them

a + b − pa − pb

(a + b ) − p(a +b) group in pairs

(a + b )(1 − p) factored form

When a polynomial is factored, we “factored out” the common factor.

Example 3.24

Factorise the following:

(i) am + bm +cm (ii) a ³ − a²b (iii) 5a − 10b − 4bc + 2ac (iv) x + y −1 –xy

Solutions

(i) am + bm +cm

am + bm +cm

m (a + b +c) factored form

(ii) a ³ − a²b

 a ² ⋅ a − a ² ⋅b group in pairs

 a ² × (a −b) factored form

(iii) 5a − 10b − 4bc + 2ac

5a − 10b + 2ac − 4bc

5(a − 2b) + 2c(a −2b)

(a − 2b )(5 + 2c)

(iv) x + y −1 −xy

x − 1 +y –xy

(x − 1) +y(1 −x)

(x − 1) -y(x -1)

(x − 1)(1 -y)

 (a − b ) = − (b-a)