Solving by Graphical Method

Solving by Graphical Method

Already we have seen graphical representation of linear equation in two variables. Here we shall learn, how we are graphically representing a pair of linear equations in two variables and find the solution of simultaneous linear equations.

Example 3.44

Use graphical method to solve the following system of equations: x + y = 5; 2x – y = 4.

Solution

Given

x + y = 5 ...(1)

2x – y = 4 ...(2)

To draw the graph (1) is very easy. We can find the x and y values and thus two of the points on the line (1).

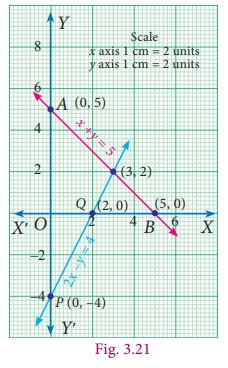
When x = 0, (1) gives y = 5.

Thus A(0,5) is a point on the line.

When y = 0, (1) gives x = 5.

Thus B(5,0) is another point on the line.

 Plot A and B ; join them to produce the line (1).

To draw the graph of (2), we can adopt the same procedure.

When x = 0, (2) gives y = −4.

Thus P(0,−4) is a point on the line.

When y = 0, (2) gives x = 2.

Thus Q(2,0) is another point on the line.

Plot P and Q ; join them to produce the line (2).

The point of intersection (3, 2) of lines (1) and (2) is a solution.

The solution is the point that is common to both the lines. Here we find it to be (3,2). We can give the solution as x = 3 and y = 2.

Note

It is always good to verify if the answer obtained is correct and satisfies both the given equations.

Example 3.45

Use graphical method to solve the following system of equations: 3x + 2y = 6; 6x + 4y = 8

Solution

Let us form table of values for each line and then fix the ordered pairs to be plotted.

When we draw the graphs of these two equations, we find that they are parallel and they fail to meet to give a point of intersection. As a result there is no ordered pair that can be common to both the equations. In this case there is no solution to the system.

Example 3.46

Use graphical method to solve the following system of equations: y= 2x + 1; −4x + 2y = 2

Solution

Let us form table of values for each line and then fix the ordered pairs to be plotted.

Graph of y = 2x + 1

Graph of −4x + 2y = 2

2y = 4x + 2

y = 2x + 1

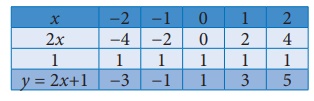
Points to be plotted :

(−2, −3), (−1, −1), (0,1), (1,3), (2, 5)

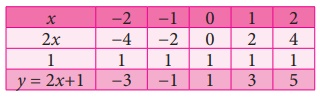
Points to be plotted :

(−2, −3), (−1, −1), (0, 1), (1, 3), (2, 5)

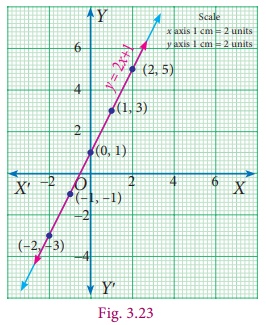
Here both the equations are identical; they were only represented in different forms. Since they are identical, their solutions are same. All the points on one line are also on the other!

This means we have an infinite number of solutions which are the ordered pairs of all the points on the line.

Example 3.47

The perimeter of a rectangle is 36 metres and the length is 2 metres more than three times the width. Find the dimension of rectangle by using the method of graph.

Solution

Let us form equations for the given statement.

Let us consider l and b as the length and breadth of the rectangle respectively.

Now let us frame the equation for the first statement

Perimeter of rectangle = 36

2(l + b) = 36

l + b = 36/2

l = 18 – b          …..(1)

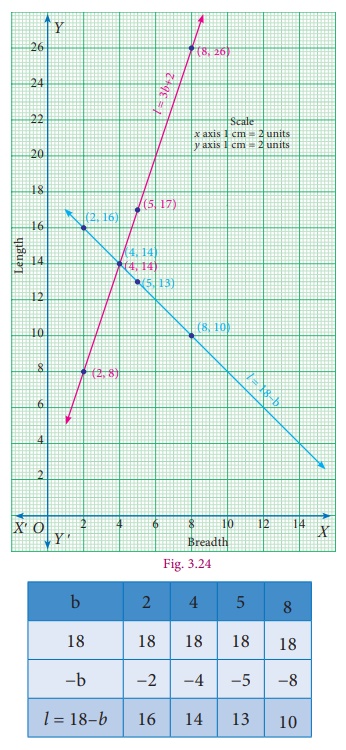
Points: (2,16), (4,14), (5,13), (8,10)

The second statement states that the length is 2 metres more than three times the width which is a straight line written as l = 3b + 2         ... (2)

Now we shall form table for the above equation (2).

Points: (2,8), (4,14), (5,17), (8,26)

The solution is the point that is common to both the lines. Here we find it to be (4,14).

We can give the solution to be b = 4, l = 14.

Verification :