Division of Polynomials

Division of Polynomials

Let us consider the numbers 13 and 5. When 13 is divided by 5 what is the quotient and remainder.?

Yes, of course, the quotient is 2 and the remainder is 3. We write 13 = (5×2)+3

Let us try.

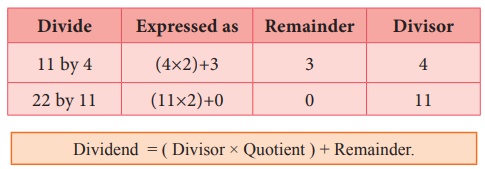
Dividend = ( Divisor × Quotient ) + Remainder.

From the above examples, we observe that the remainder is less than the divisor.

1. Division Algorithm for Polynomials

Let p(x) and g(x) be two polynomials such that degree of p(x) > degree of g(x) and g(x) ≠ 0.

Then there exists unique polynomials q(x) and r(x) such that

 p(x) = g (x ) × q (x ) + r (x ) … (1)

where r(x) = 0 or degree of r(x) < degree of g(x).

The polynomial p(x) is the Dividend, g(x) is the Divisor, q(x) is the Quotient and r(x) is the Remainder. Now (1) can be written as

Dividend = ( Divisor × Quotient ) + Remainder.

If r(x) is zero, then we say p(x) is a multiple of g(x). In other words, g(x) divides p(x).

If it looks complicated, don’t worry! it is important to know how to divide polynomials, and that comes easily with practice. The examples below will help you.

Example 3.32

Divide x³ − 4x² + 6x by x, where , x ≠ 0

Solution

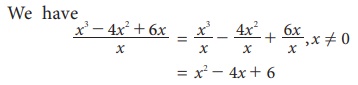
Example 3.33

Find the quotient and the remainder when (5x² − 7x + 2) ÷ (x − 1)

Solution

(5x² − 7x + 2) ÷ (x − 1)

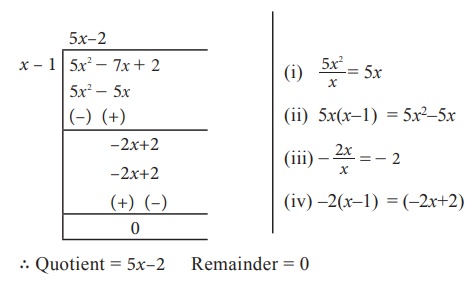
∴ Quotient = 5x–2

Remainder = 0

Example 3.34

Find quotient and the remainder when f(x) is divided by g(x)

(i) f(x) = (8x³–6x²+15x–7), g(x) = 2x+1.

(ii) f(x) = x⁴ –3x³ + 5x² –7, g(x) = x² + x + 1

Solution

(i) f(x) = (8x³–6x²+15x–7), g(x) = 2x+1

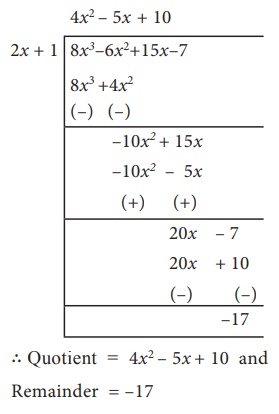
(ii) f(x) = x⁴ –3x³ + 5x² –7, g(x) = x² + x + 1

2. Synthetic Division

Synthetic Division is a shortcut method of polynomial division. The advantage of synthetic division is that it allows one to calculate without writing variables, than long division.

Example 3.35

Find the quotient and remainder when p(x ) = (3x ³ −2x ² – 5 + 7x) is divided by d(x) = x + 3 using synthetic division.

Solution

Step 1

Arrange dividend and the divisor in standard form.

3x ³ − 2x² + 7x −5 (standard form of dividend)

x + 3 (standard form of divisor)

Write the coefficients of dividend in the first row. Put ‘0’ for missing term(s).

 3 −2      7 −5 (first row)

Step 2 Find out the zero of the divisor.

 x + 3 = 0 implies x = −3

Step 3 Write the zero of divisor in front of dividend in the first row. Put ‘0’ in the first  column of second row.

Step 4 Complete the second row and third row as shown below.

All the entries except the last one in the third row are the coefficients of the quotient.

Then quotient is 3x ² −11x + 40 and and remainder is -125.

Example 3.36

Find the quotient and remainder when (3x ^{3 −} 4x² − 5) is divided by (3x+1) using synthetic division.

Solution

Let p(x) = 3x³ − 4x² − 5, d(x) = (3x +1)

Standard form: p(x) = 3x ³ − 4x² + 0x −5

and d (x) = 3x +1

Example 3.37

If the quotient on dividing x⁴ + 10x³ + 35x² + 50x + 29 by (x + 4) is x³ − ax² +bx + 6 , then find the value of a, b and also remainder.

Solution

Let p(x) = x⁴ +10x³ + 35x² + 50x + 29

Standard form = x⁴ +10x³ + 35x² + 50x + 29

quotient x ³ + 6x² +11x + 6 is compared with given quotient x ³ − ax ² +bx + 6

coefficient of x² is 6 = −a and coefficient of x is 11 = b

Therefore, a = −6 , b = 11 and remainder = 5 .