Exercise 3.3: Remainder Theorem

Exercise 3.3: Remainder Theorem

1. Check whether p(x) is a multiple of g(x) or not .

 p(x) = x³ − 5x² + 4x − 3 ; g(x) = x – 2

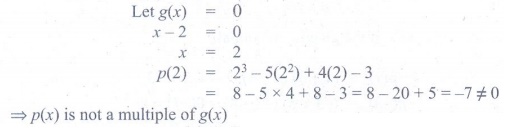
2. By remainder theorem, find the remainder when, p(x) is divided by g(x) where,

(i) p(x) = x³ − 2x² − 4x − 1 ; g( x ) = x + 1

(ii) p(x) = 4x³ − 12x² + 14 x − 3; g( x ) = 2 x − 1

(iii) p(x) = x³ − 3x² + 4x + 50 ; g( x ) = x − 3

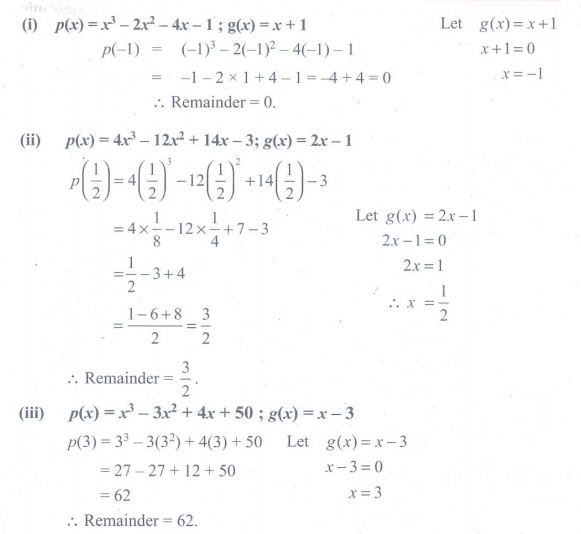
3. Find the remainder when 3x³ − 4x² + 7x − 5 is divided by (x+3)

4. What is the remainder when x²⁰¹⁸ +2018 is divided by x–1

5. For what value of k is the polynomial

 p ( x) = 2x³ − kx² + 3x + 10 exactly divisible by (x–2)

6. If two polynomials 2x³ + ax² + 4x – 12 and x³ + x² –2x+ a leave the same remainder when divided by (x – 3), find the value of a and also find the remainder.

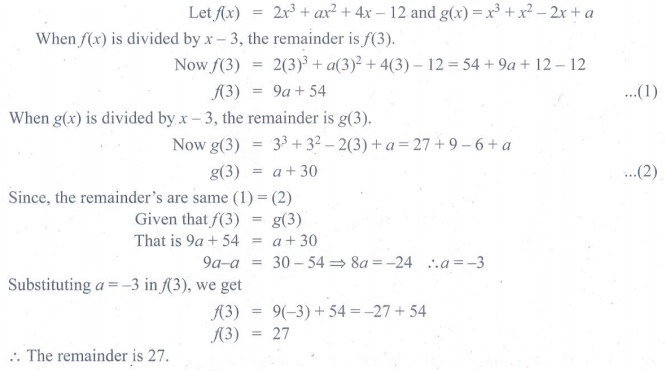
7. Determine whether (x -1) is a factor of the following polynomials:

i) x ³ + 5x ² – 10x + 4 ii) x ⁴ + 5x ² – 5x +1

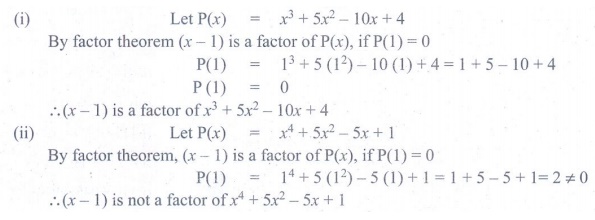
8. Using factor theorem, show that (x − 5) is a factor of the polynomial 2x ³ − 5x² −28x + 15

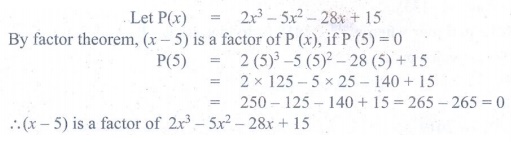
9. Determine the value of m , if (x + 3) is a factor of x³ − 3x² −mx + 24 .

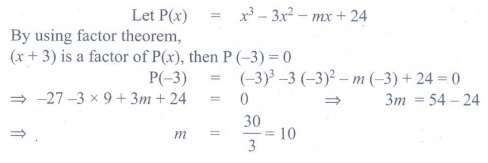
10. If both (x -2) and (x – 1/2) are the factors of ax² + 5x +b , then show that a = b.

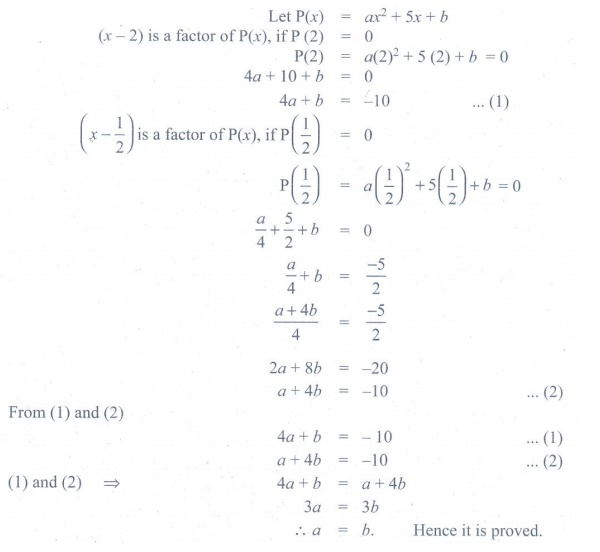
11. If (x -1) divides the polynomial kx ³ − 2x² + 25x −26 without remainder, then find the value of k .

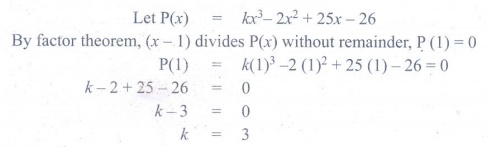
12. Check if (x + 2) and (x − 4) are the sides of a rectangle whose area is x² – 2x – 8 by using factor theorem.